Zależności kątów w trójkącie

W czasie studiów budowlanych wiele razy spotykamy się z problemem, gdy jakaś siła, obciążenie lub podpora występują pod kątem. W takiej sytuacji warto się zapoznać z podstawowymi zależnościami kątowymi oraz ich wartościami najczęściej używanymi w obliczeniach.

Podstawowe funkcje trygonometryczne

Mamy cztery podstawowe zależności w trójkącie prostokątnym:

• sinus ($\sin$)
• cosinus ($\cos$)
• tangens ($\text{tg}$)
• cotangens ($\text{ctg}$)

Trójkąt prostokątny

Dla trójkąta prostokątnego o bokach $a$, $b$ (przyprostokątne) i $x$ (przeciwprostokątna) oraz kącie $\alpha$:

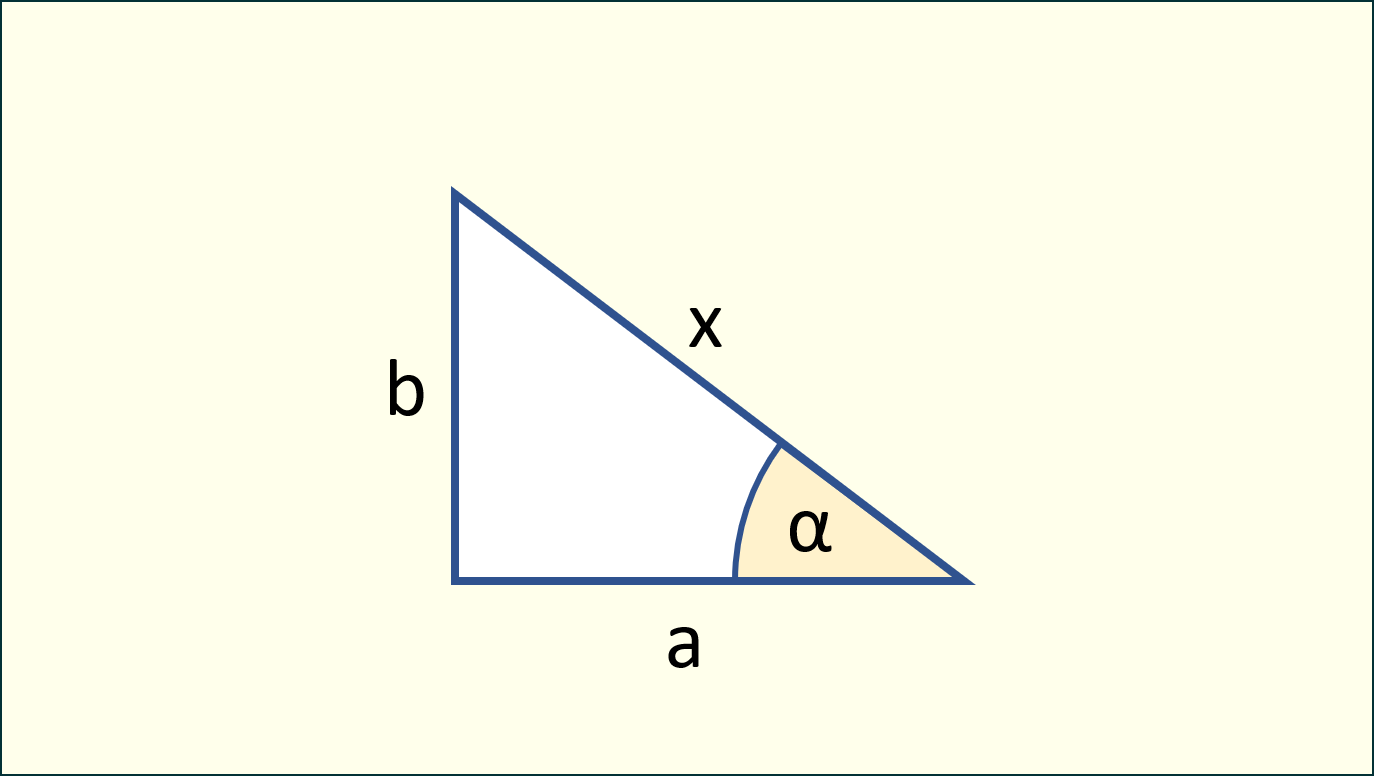
Definicje

Sinus ($\sin \alpha$) jest równy stosunkowi przyprostokątnej znajdującej się naprzeciwko kąta do przeciwprostokątnej trójkąta:

Cosinus ($\cos \alpha$) jest równy stosunkowi przyprostokątnej leżącej przy kącie do przeciwprostokątnej trójkąta:

Tangens ($\text{tg} \, \alpha$) jest równy stosunkowi przyprostokątnej znajdującej się naprzeciwko kąta do przyprostokątnej leżącej przy kącie:

Cotangens ($\text{ctg} \, \alpha$) jest równy stosunkowi przyprostokątnej leżącej przy kącie do przyprostokątnej znajdującej się naprzeciwko kąta:

Warto znać i rozumieć powyższe zależności, ponieważ są one bardzo często używane zarówno podczas obliczeń inżynierskich i prac wykonawczych.

Wartości funkcji trygonometrycznych dla wybranych kątów

Podstawowe wartości dla kątów $0°$, $30°$, $45°$, $60°$ oraz $90°$: