Kącik Wiedzy
Wykresy sił wewnętrznych i ich wzory dla układów prostych

Wykresy sił wewnętrznych i ich wzory dla układów prostych

maja 22, 2018

Dla niektórych prostych elementów konstrukcyjnych jesteśmy w stanie wyznaczyć wykresy sił wewnętrznych i ich wartości korzystając z prostych wzorów. Jest to niezwykle użyteczne i pozwala nam z mniejszą lub większą dokładnością oszacować jak wykres powinien wyglądać nawet w bardziej skomplikowanych elementach.

Belki wspornikowe

Siła skupiona

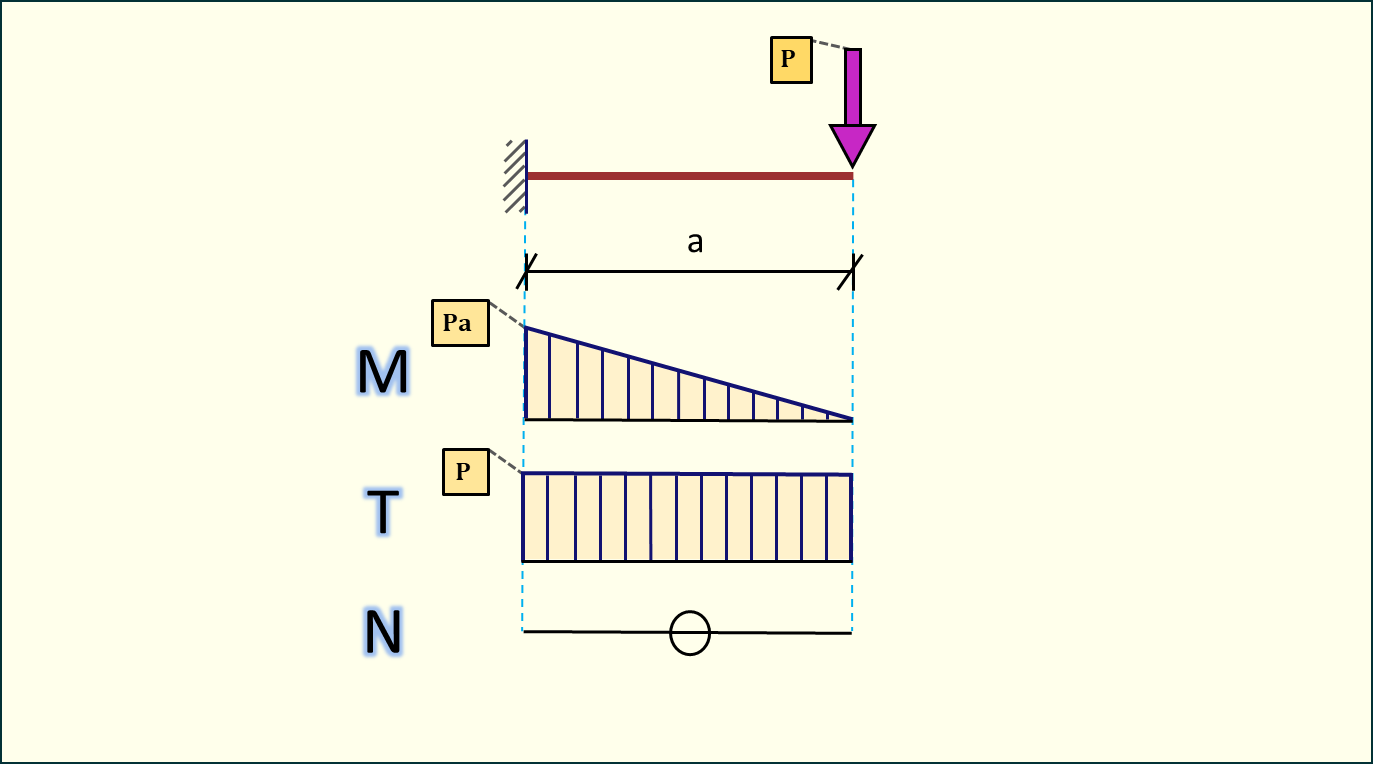
Rys. 1. Siła skupiona w belce wspornikowej

Schemat ten jest bardzo prosty i w zasadzie wszystko sprowadza się do obliczenia reakcji we wsporniku.

Moment przyłożony

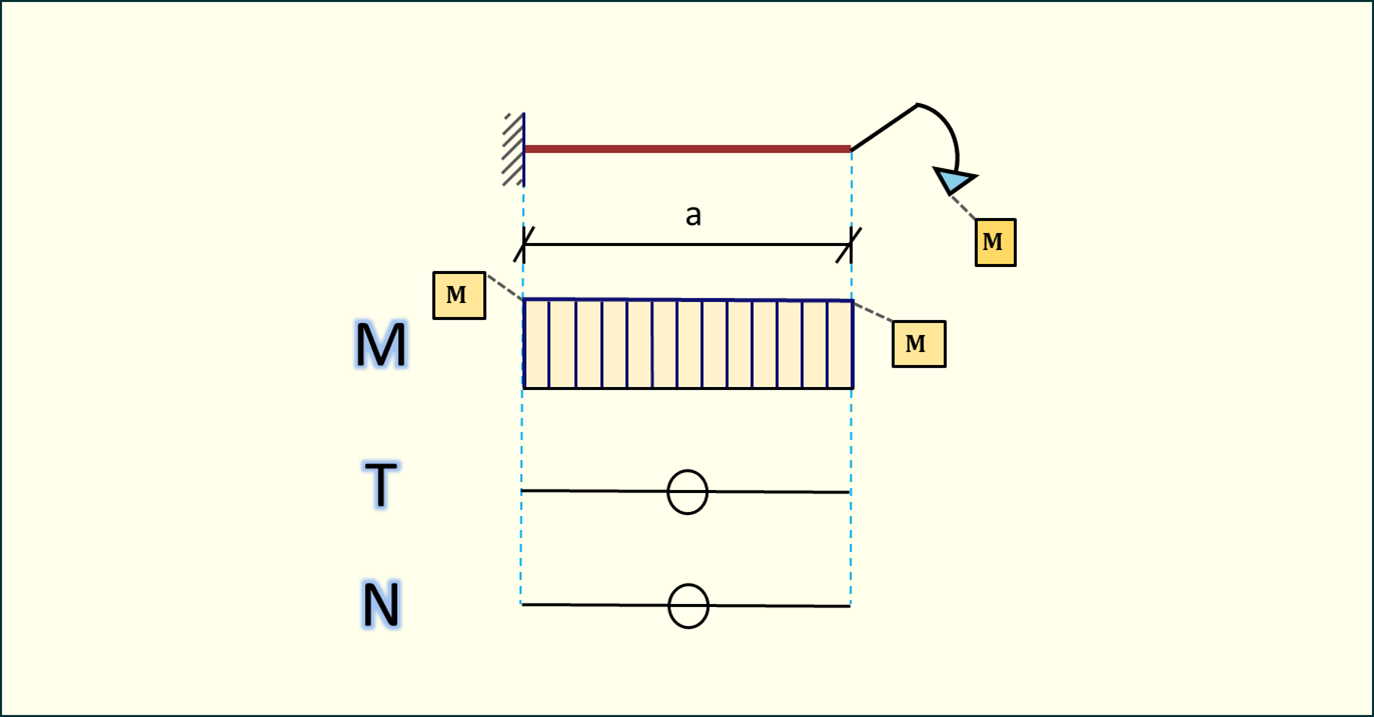
Rys. 2. Moment skupiony w belce wspornikowej

Na element działa tylko moment skupiony, więc moment we wsporniku będzie go równoważył.

Siła równomiernie rozłożona

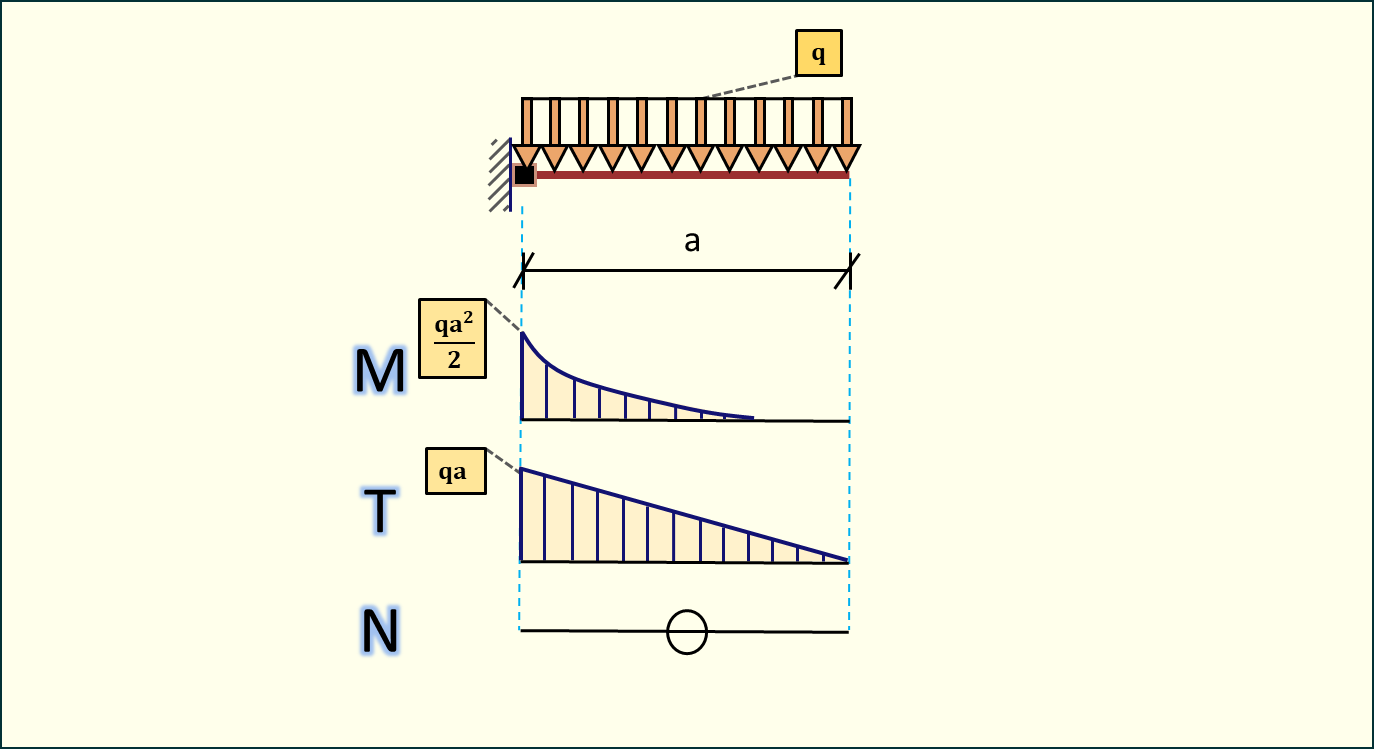
Rys. 3. Belka wspornikowa z obciążeniem równomiernie rozłożonym

Wartość momentu będzie równa wartości siły równomiernie rozłożonej pomnożonej przez odległość, na której ona działa oraz połowę tej odległości. Wypadkowa tej siły wypada idealnie w środku, zatem ramię, na którym działa moment jest równe połowie długości, na której działa siła równomiernie rozłożona. Innymi słowy:

M=q⋅a⋅12⋅a=q⋅a22M = q \cdot a \cdot \frac{1}{2} \cdot a = \frac{q \cdot a^2}{2}

Wartość siły tnącej jest równa wartości siły wypadkowej obciążenia.

Belki swobodnie podparte

Moment skupiony

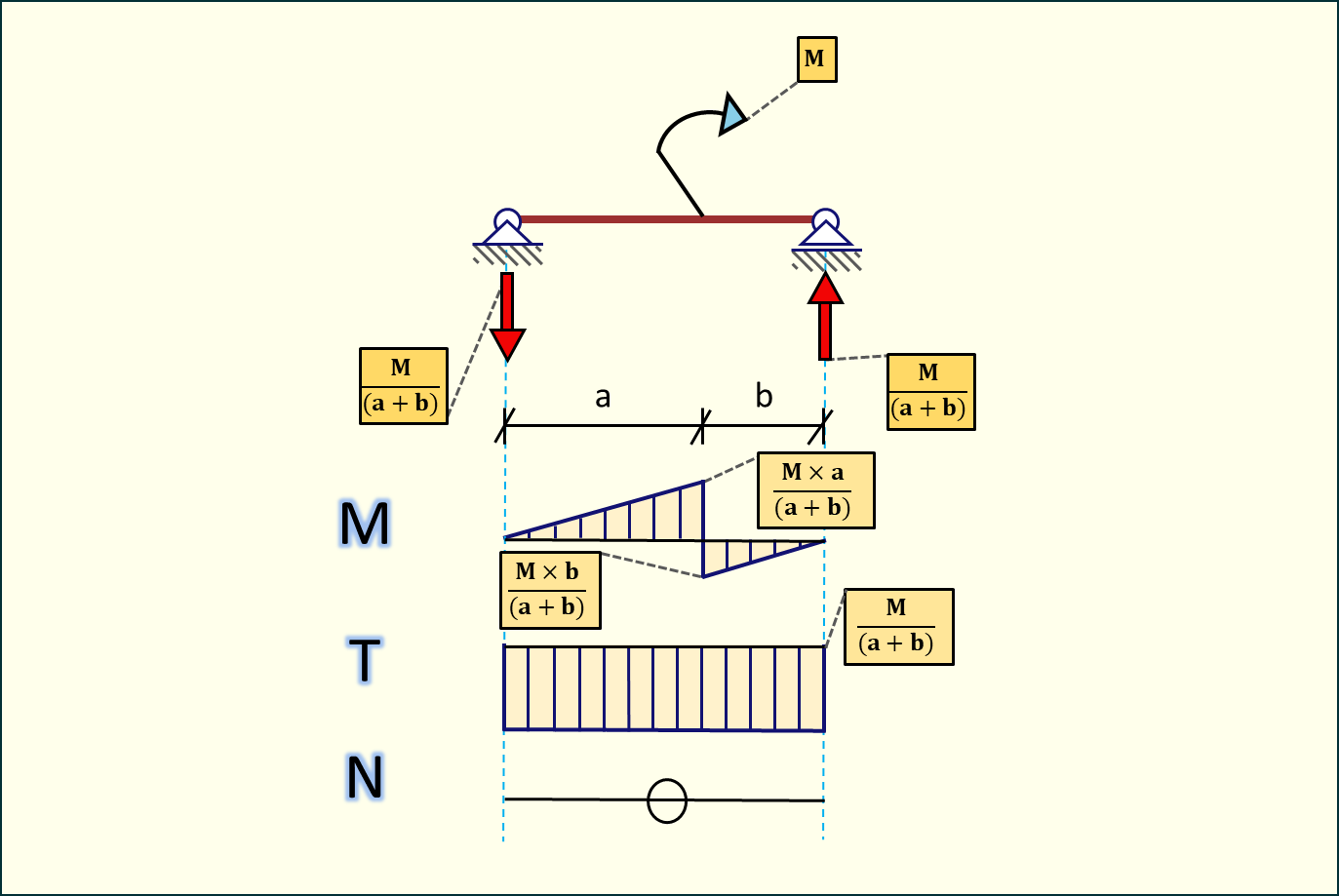
Rys. 4. Belka swobodnie podparta z momentem skupionym

Wartość reakcji podporowych jest równa wartości momentu podzielonej przez długość całkowitą belki. Siły tnące równe są wartości reakcji podporowych. Wartości momentów liczymy mnożąc wartość reakcji podporowej przez odległość pomiędzy podporą, a punktem przyłożenia momentu.

Siła skupiona

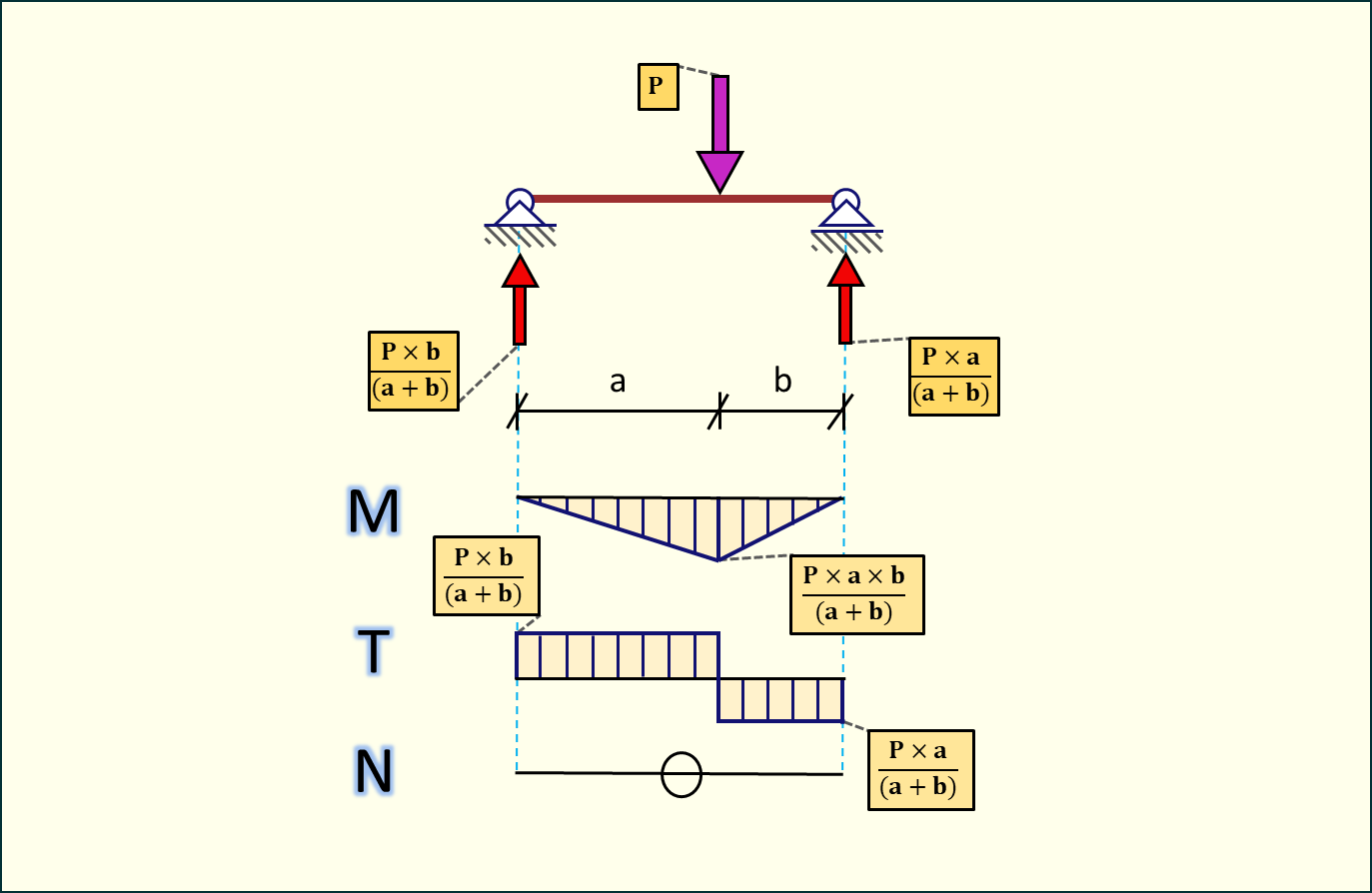
Rys. 5. Belka swobodnie podparta z siłą skupioną

Na początek spróbujmy policzyć reakcje w tej belce i sprawdzmy czy wzory są poprawne.

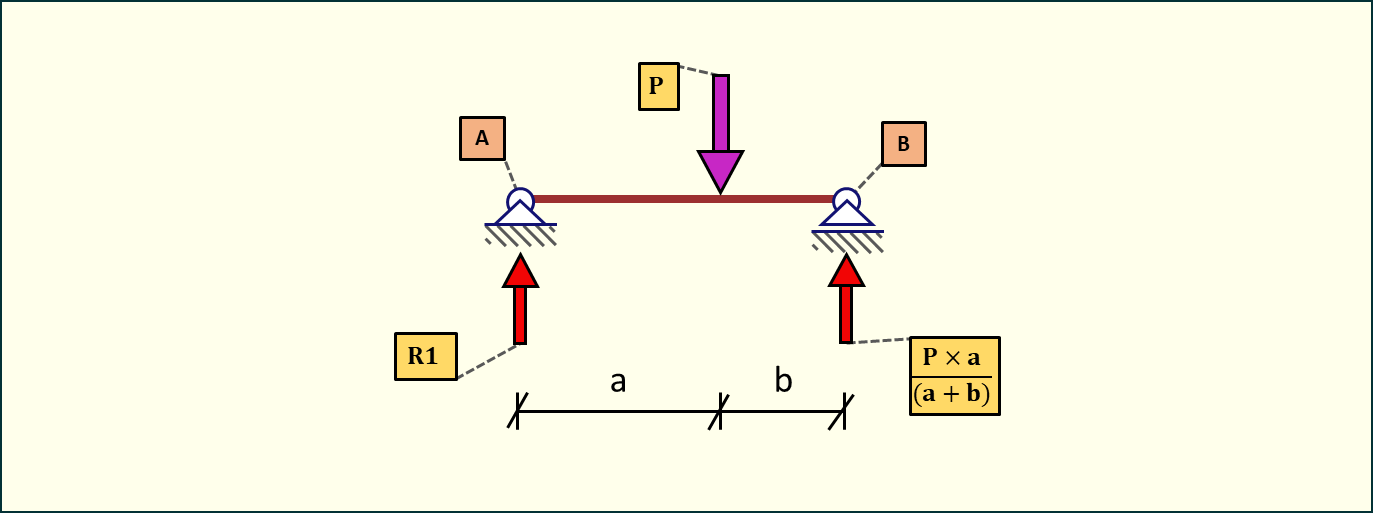
Rys. 6. Reakcja podporowa VA (R1)

Rozpoczniemy z pierwsza reakcją podporową VA (oznaczona jako R1R1 na powyższym rysunku):

∑MB=0\sum M_B = 0

VA⋅(a+b)−P⋅b=0V_A \cdot (a + b) - P \cdot b = 0

VA⋅(a+b)=P⋅bV_A \cdot (a + b) = P \cdot b

VA=P⋅ba+bV_A = \frac{P \cdot b}{a + b}

Następnie policzmy reakcje podporową VB (oznaczona jako R2R2 na poniższym rysunku rysunku):

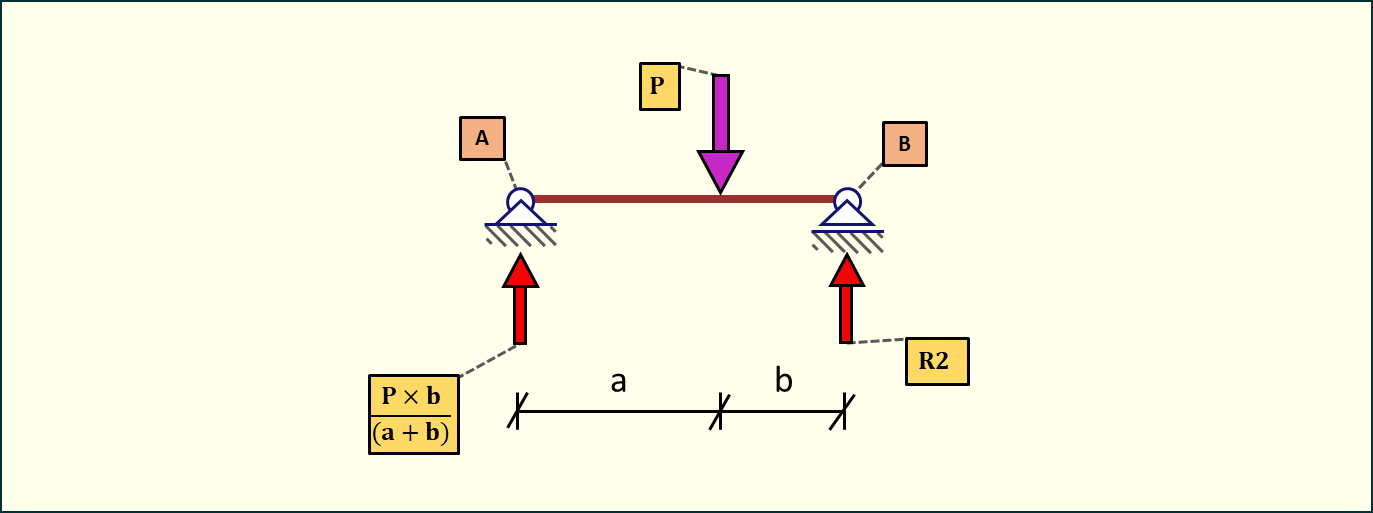
Rys. 7. Reakcja podporowa VB (R2)

∑MA=0\sum M_A = 0

−VB⋅(a+b)+P⋅a=0-V_B \cdot (a + b) + P \cdot a = 0

VB⋅(a+b)=P⋅aV_B \cdot (a + b) = P \cdot a

VB=P⋅aa+bV_B = \frac{P \cdot a}{a + b}

Widzimy zatem, że wzory na reakcje podporowe są poprawne. Spróbujmy policzyć wartość maksymalną momentu.

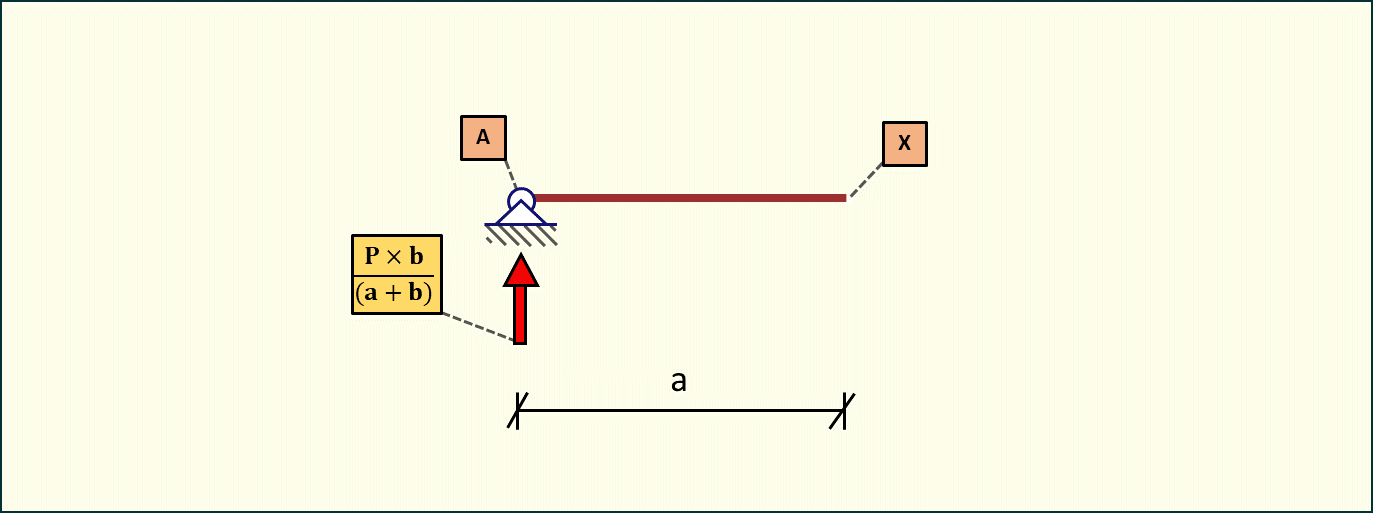
Rys. 8. Maksymalny moment

Mmax=VA⋅a=P⋅b⋅aa+bM_{max} = V_A \cdot a = \frac{P \cdot b \cdot a}{a + b}

Zatem maksymalny moment jest równy iloczynowi wartości reakcji podporowej oraz odległości od podpory. Wzór jest zgodny. Jako ostatnie zostały nam wartości sił tnących. Są one równe wartości reakcji podporowych.

Obciążenie równomiernie rozłożone

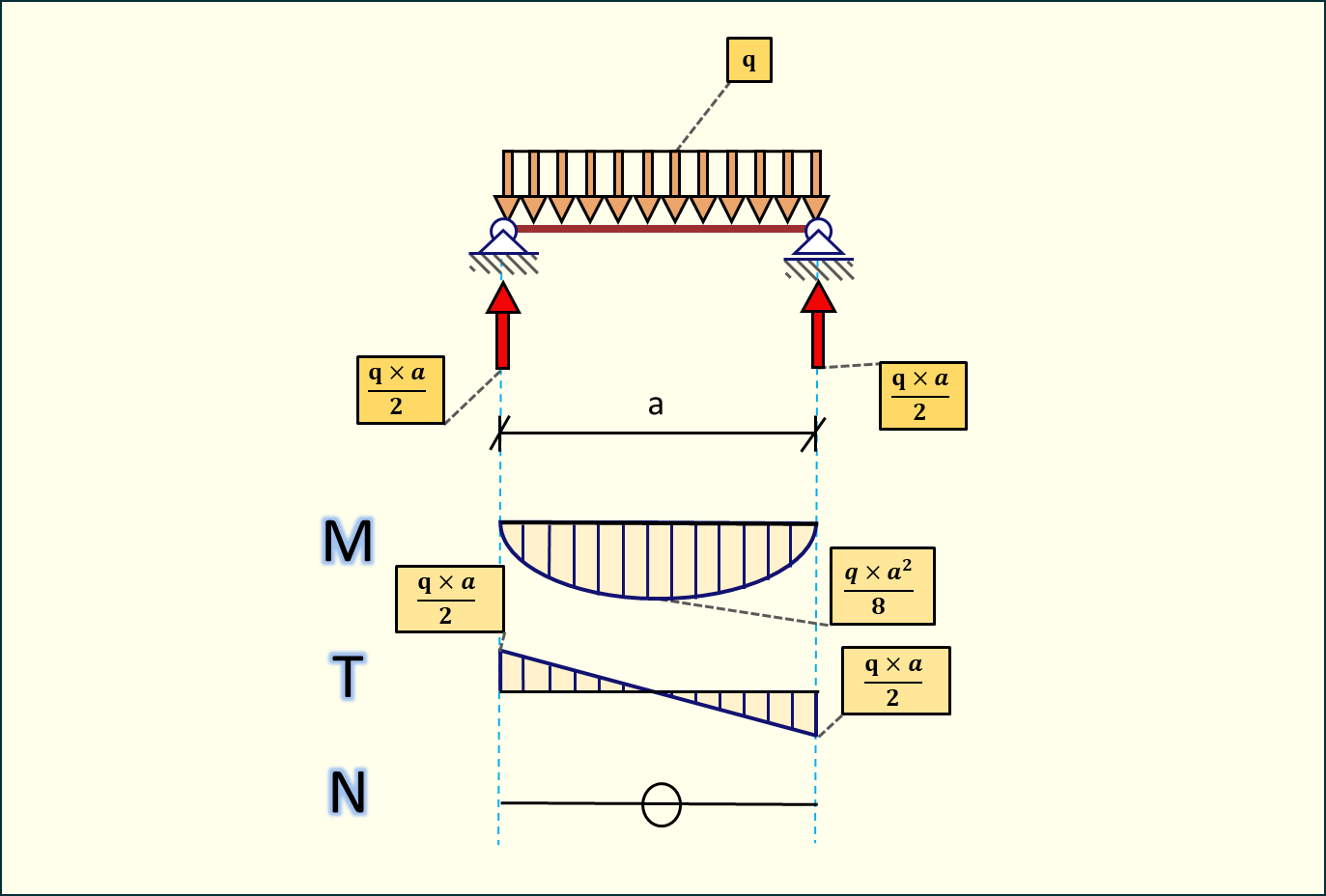
Rys. 9. Belka swobodnie podparta z obciążeniem równomiernie rozłożonym

Wartości reakcji podporowych są równe wartości siły wypadkowej podzielonej przez dwa, ponieważ obciążenie jest przekazywane jednakowo na każdą z dwóch podpór. Wartości sił tnących równe są reakcjom podporowym. Moment obliczymy jako iloczyn siły wypadkowej obciążenia przyłożonej w połowie długości elementu i jej odległości od podpory. Mamy zatem:

∑M=q⋅a2⋅12⋅a\sum M = \frac{q \cdot a}{2} \cdot \frac{1}{2} \cdot a

Pierwsza wartość to reakcja podporowa, która jest stała. Druga natomiast to połowa odległości, na której rozpatrujemy działanie obciążenia. My chcemy znać moment równo w środku przęsła, więc za drugie a musimy podstawić połowę tej wartości. Zatem:

Mmax=q⋅a2⋅12⋅12⋅a=q⋅a28M_{max} = \frac{q \cdot a}{2} \cdot \frac{1}{2} \cdot \frac{1}{2} \cdot a = \frac{q \cdot a^2}{8}

Wszystko się zgadza. Warto znać te wzory oraz wiedzieć skąd się biorą. Z czasem są one nieocenioną pomocą w trakcie obliczeń i pozwalają wyrobić sobie nawyk przewidywania kształtu wykresów w skomplikowanych elementach.

Ostatnia aktualizacja:
Moment zginającyBelka statycznie wyznaczalna - przykład krok po kroku