Kącik Wiedzy
Siła skupiona

Siła skupiona

maja 22, 2018

Siła skupiona to obciążenie działające w jednym punkcie elementu konstrukcyjnego. Gdy siła działa pod kątem, można ją rozłożyć na składowe wzdłuż osi układu współrzędnych.

Rozkład siły na składowe

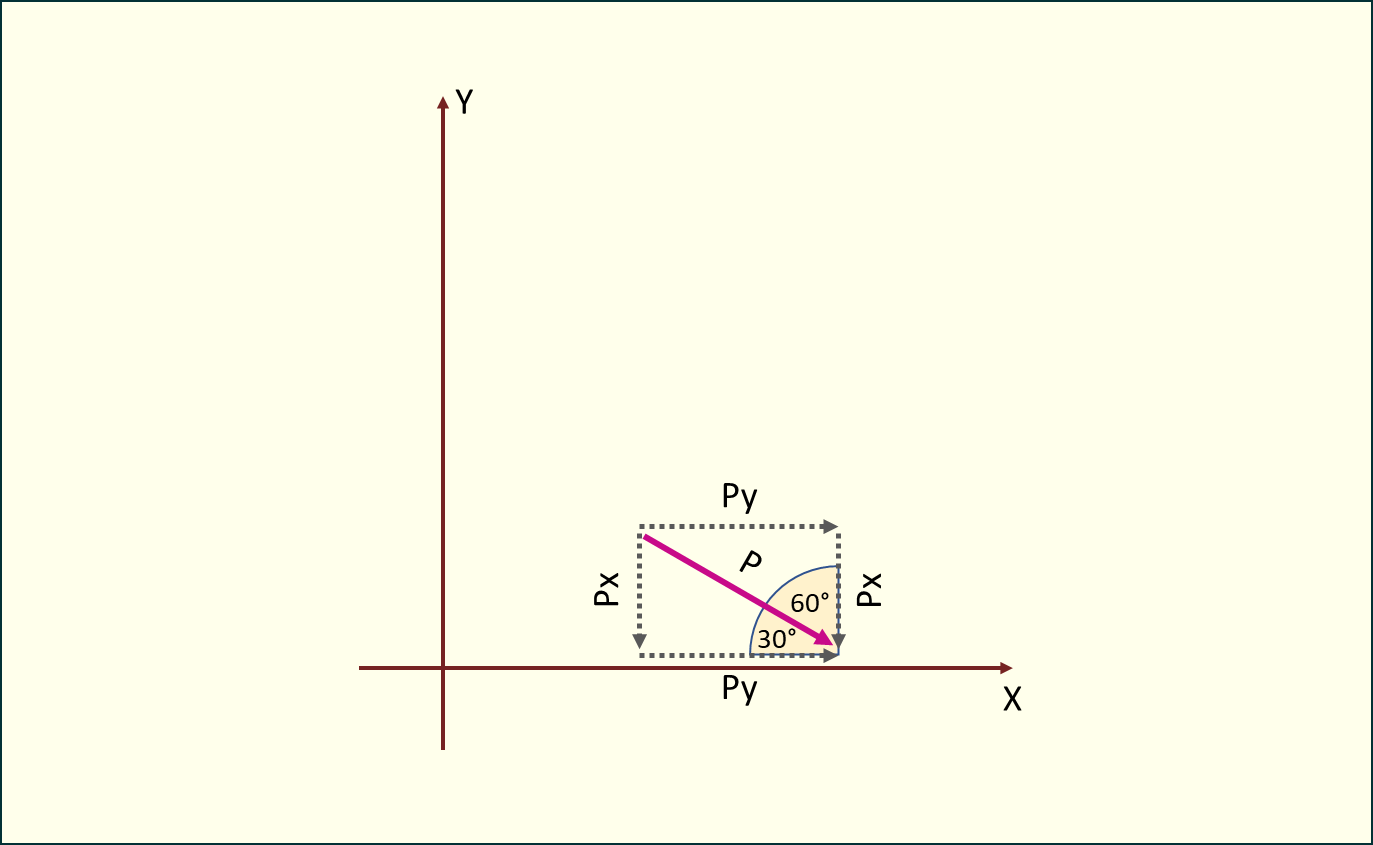
Rys. 1. Rozkład siły skupionej pod kątem na składowe Px i Py

Siłę działającą pod kątem α\alpha możemy rozłożyć na dwie składowe:

  • Składowa PxP_x – działa prostopadle do elementu (na oś XX)
  • Składowa PyP_y – działa równolegle do elementu (na oś YY)

Zależności trygonometryczne

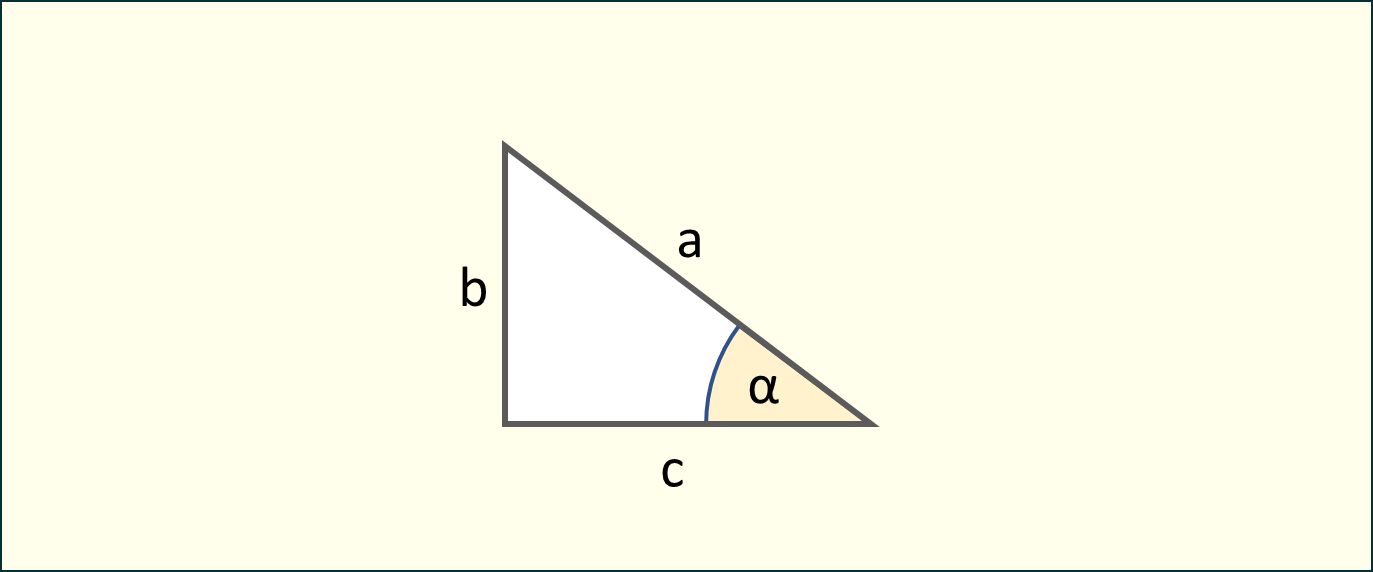
Rys. 2. Trójkąt prostokątny ilustrujący zależności trygonometryczne

Do obliczenia wartości siły w danym kierunku wykorzystuje się zależności kątowe:

sin⁡α=ba→b=a⋅sin⁡α\sin \alpha = \frac{b}{a} \rightarrow b = a \cdot \sin \alphacos⁡α=ca→c=a⋅cos⁡α\cos \alpha = \frac{c}{a} \rightarrow c = a \cdot \cos \alpha

Obliczanie składowych siły

Na podstawie Rys. 1 i zależności trygonometrycznych możemy obliczyć składowe siły PxP_x i PyP_y następująco:

Dla kąta 30°:

sin⁡30°=PxP→Px=P⋅sin⁡30°\sin 30° = \frac{P_x}{P} \rightarrow P_x = P \cdot \sin 30°cos⁡30°=PyP→Py=P⋅cos⁡30°\cos 30° = \frac{P_y}{P} \rightarrow P_y = P \cdot \cos 30°

Przykład dla P = 100 kN:

Px=100 kN⋅sin⁡30°=100 kN⋅0,5=50 kNP_x = 100\,\text{kN} \cdot \sin 30° = 100\,\text{kN} \cdot 0{,}5 = 50\,\text{kN}Py=100 kN⋅cos⁡30°=100 kN⋅0,866=86,6 kNP_y = 100\,\text{kN} \cdot \cos 30° = 100\,\text{kN} \cdot 0{,}866 = 86{,}6\,\text{kN}

Dla kąta 60°:

sin⁡60°=PyP→Py=P⋅sin⁡60°\sin 60° = \frac{P_y}{P} \rightarrow P_y = P \cdot \sin 60°cos⁡60°=PxP→Px=P⋅cos⁡60°\cos 60° = \frac{P_x}{P} \rightarrow P_x = P \cdot \cos 60°

Przykład dla P = 100 kN:

Py=100 kN⋅sin⁡60°=100 kN⋅0,866=86,6 kNP_y = 100\,\text{kN} \cdot \sin 60° = 100\,\text{kN} \cdot 0{,}866 = 86{,}6\,\text{kN}Px=100 kN⋅cos⁡60°=100 kN⋅0,5=50 kNP_x = 100\,\text{kN} \cdot \cos 60° = 100\,\text{kN} \cdot 0{,}5 = 50\,\text{kN}
Ostatnia aktualizacja:
Zasada działania sił w przegubieObciążenie rozłożone