Kącik Wiedzy
Rama statycznie wyznaczalna - krok po kroku

Rama statycznie wyznaczalna - krok po kroku

kwietnia 21, 2019

Wprowadzenie

Zadanie: Wyznaczyć reakcje i obliczyć MTN w ramie statycznie wyznaczalnej.

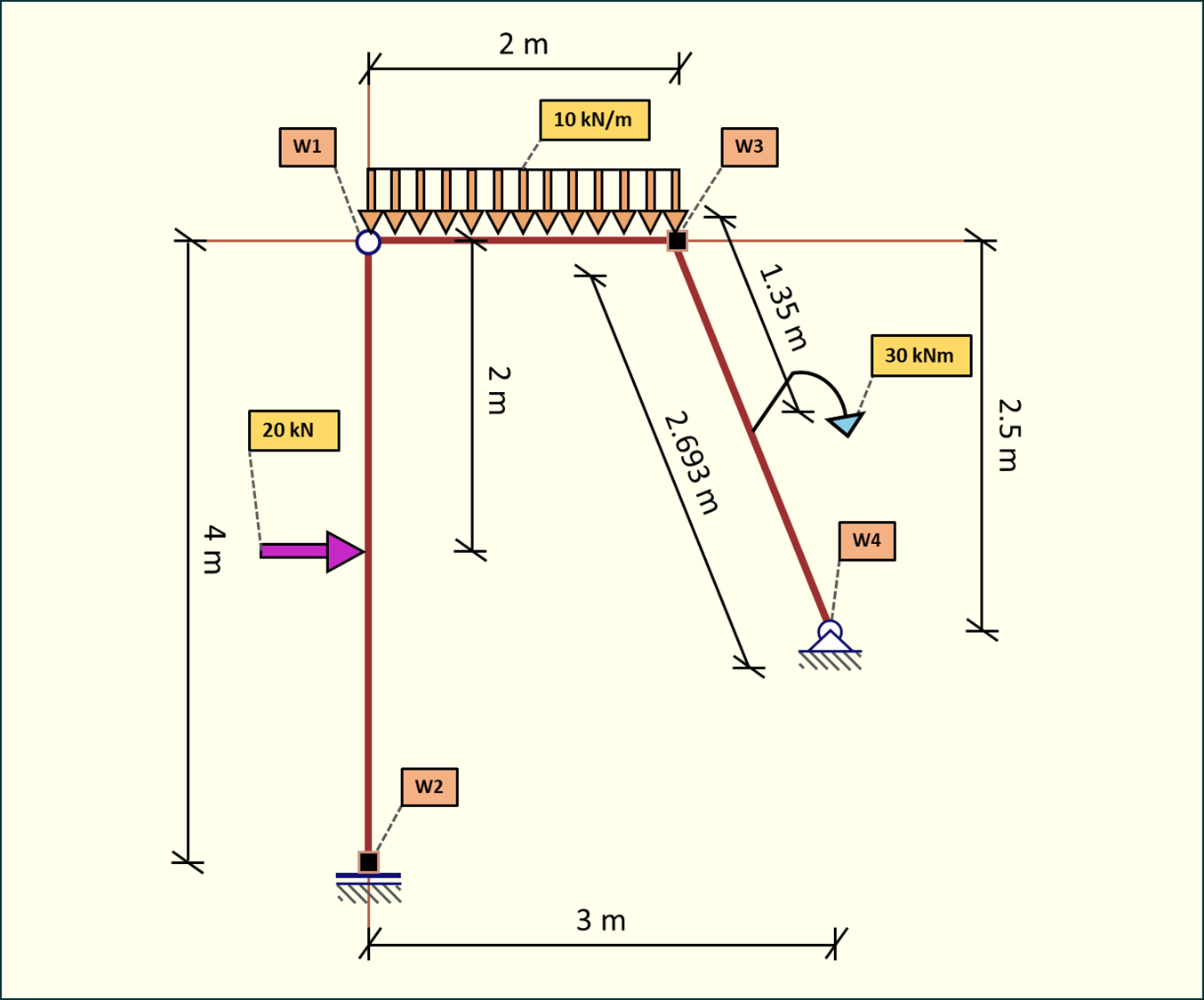
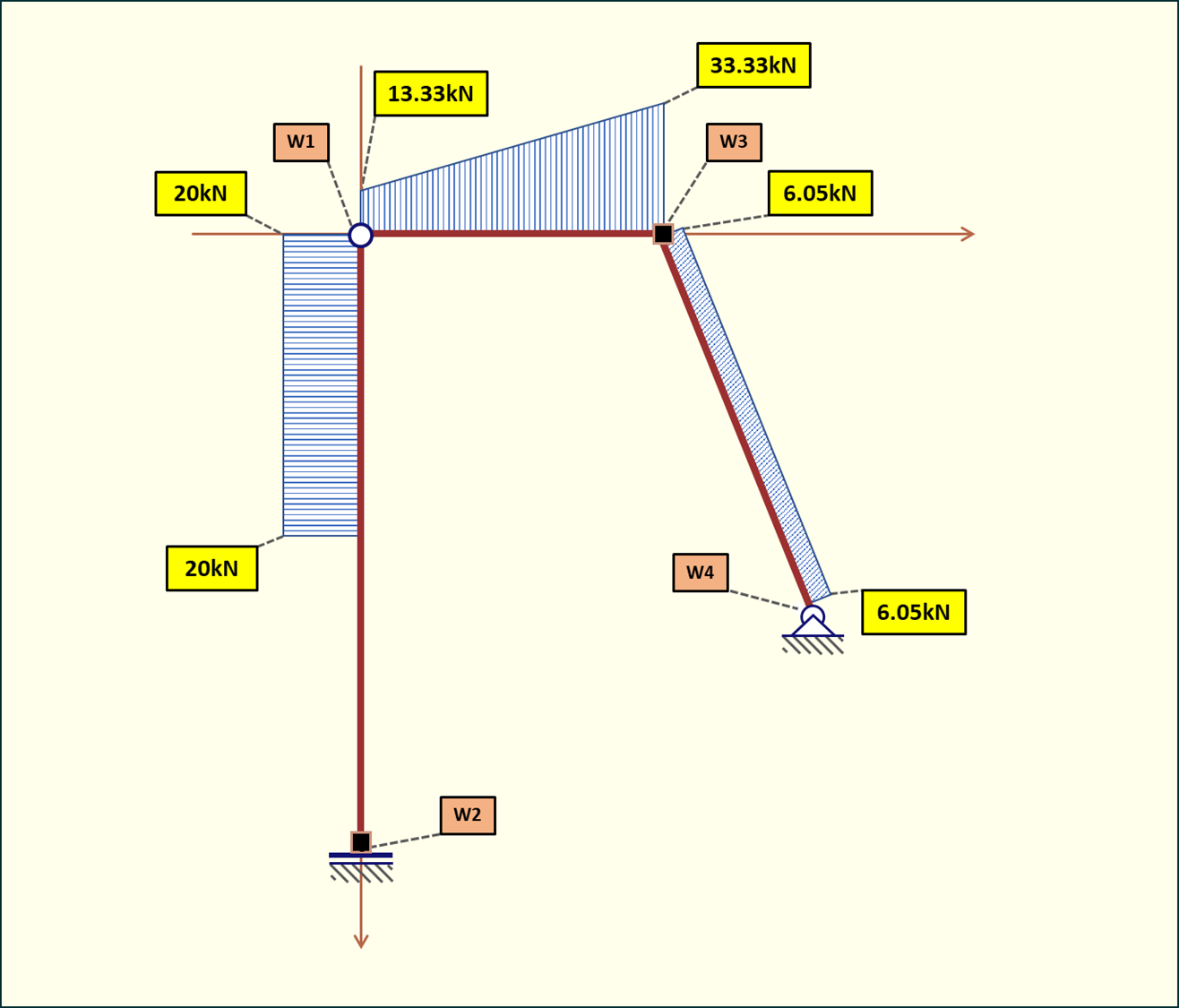
Rys. 1. Układ statyczny

1. Stopień statycznej niewyznaczalności SSN

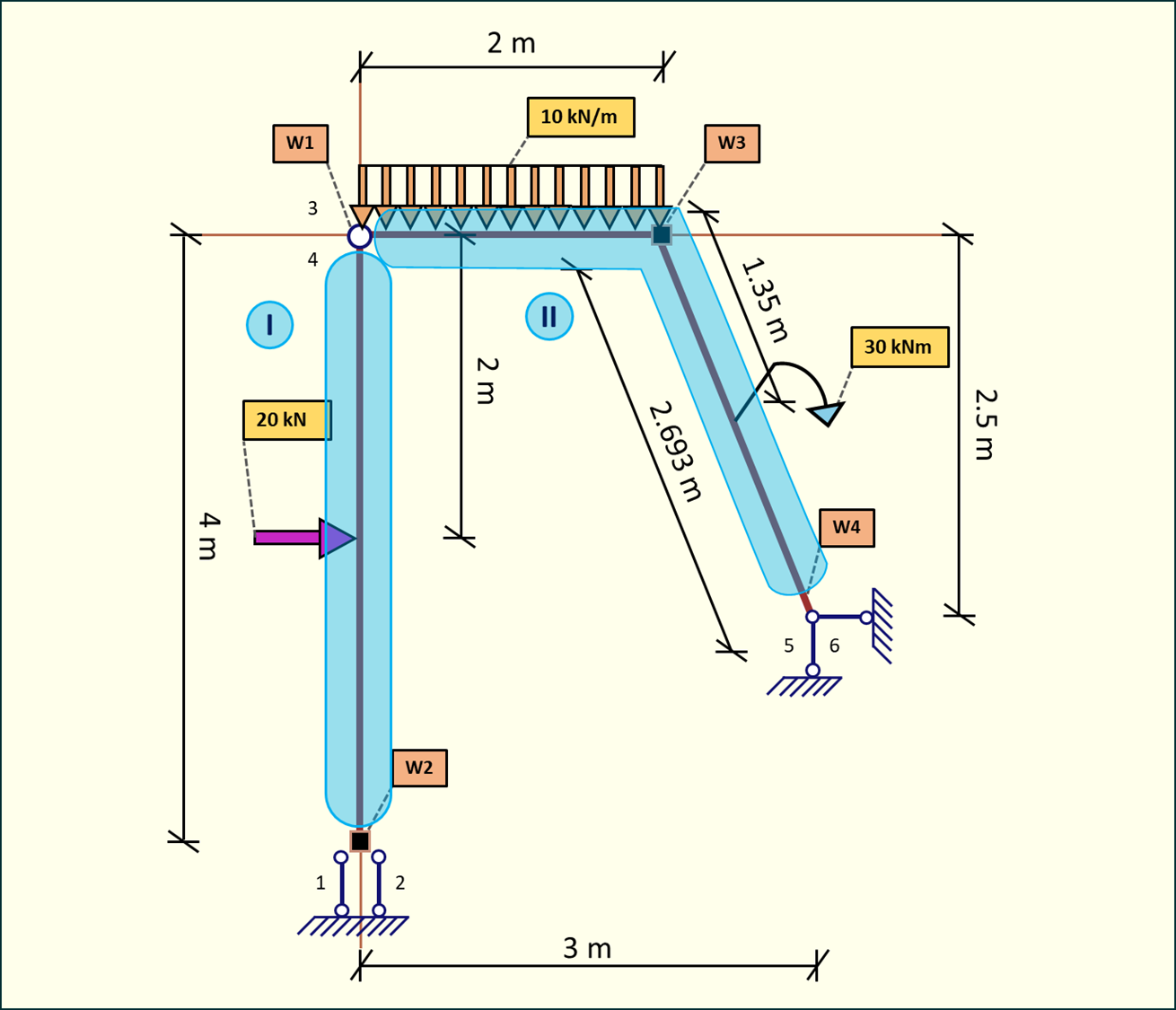
Rys. 2. Podział na tarcze

Liczba tarcz t=2
Liczba więzi n= 2+2+2=6
Wzór: 3t=n
3 * 2 = 6
6=6
Układ jest statycznie wyznaczalny.

2. Reakcje podporowe

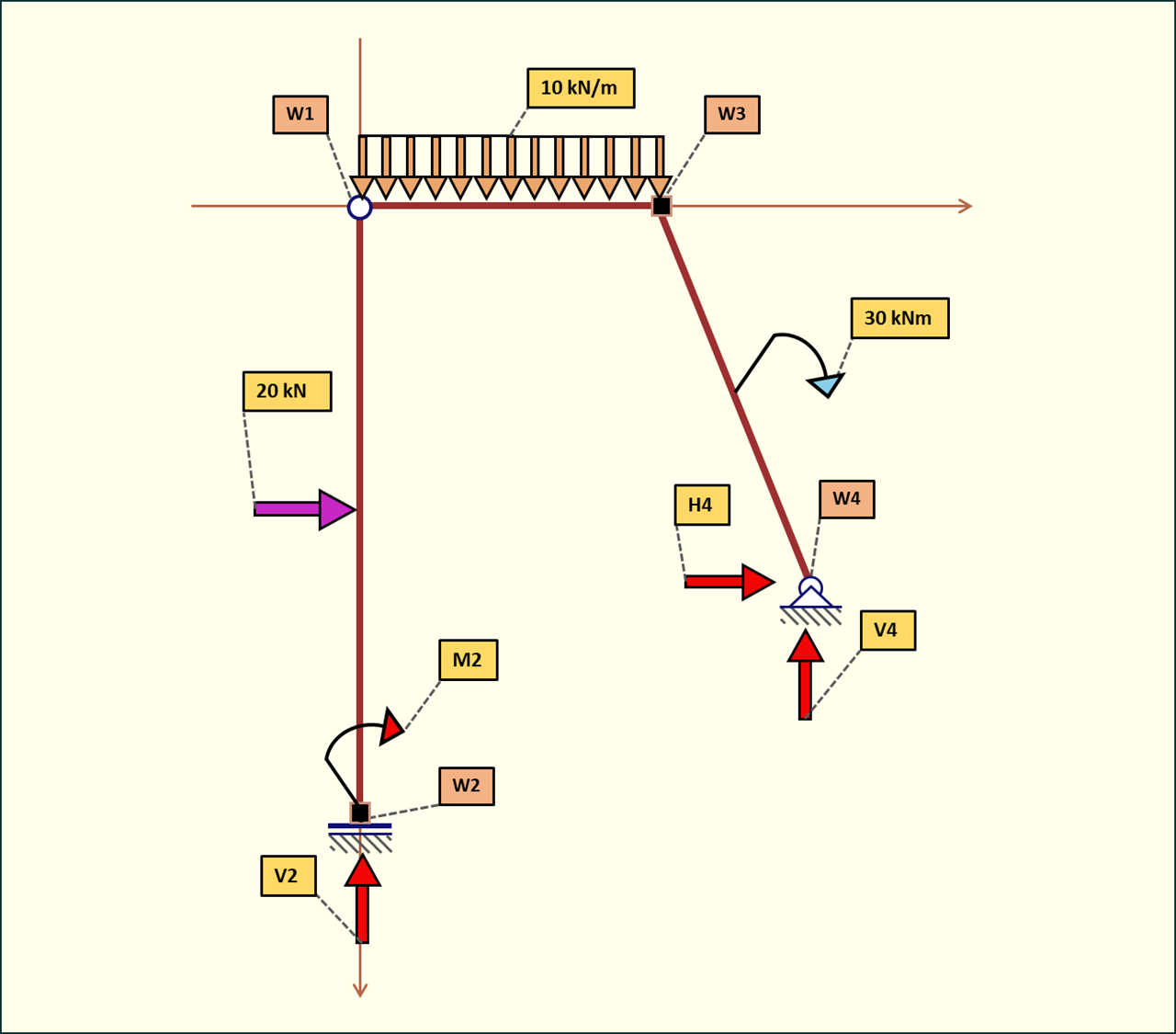
Rys. 3. Reakcje podporowe

Mamy cztery niewiadome do obliczenia: M2, V2, V4 i H4:
Tarcza nr I, część 1-2

∑MW1=0\sum M_{W1} = 0

−20kN⋅2m+M2=0-20kN \cdot 2m + M_2 = 0

M2=40kNm\mathbf{M_2 = 40kNm}

Tarcza nr II, część 1-3-4

∑Fy=0\sum F_y = 0

20kN+H4=020kN + H_4 = 0

H4=−20kN\mathbf{H_4 = -20kN}
∑MW1=0\sum M_{W1} = 0

10kN/m⋅2m⋅12⋅2m+30kNm−V4⋅3m−H4⋅2.5m=010kN/m \cdot 2m \cdot \frac{1}{2} \cdot 2m + 30kNm - V_4 \cdot 3m - H_4 \cdot 2.5m = 0

50kN−V4⋅3m−H4⋅2.5m=050kN - V_4 \cdot 3m - H_4 \cdot 2.5m = 0

50kN−3V4−(−20kN)⋅2.5m=050kN - 3V_4 - (-20kN) \cdot 2.5m = 0

50kN−3V4+50kN=050kN - 3V_4 + 50kN = 0

3V4=100kN3V_4 = 100kN

V4=33.33kN\mathbf{V_4 = 33.33kN}
∑Fx=0\sum F_x = 0

V2−2⋅10kN+V4=0V_2 - 2 \cdot 10kN + V_4 = 0

V2−20kN+33.33kN=0V_2 - 20kN + 33.33kN = 0

V2=−13.33kN\mathbf{V_2 = -13.33kN}

Lub możemy wszystko obliczyć przy pomocy układu równań:

{10kN/m⋅2m⋅12⋅2m+30kNm−V4⋅3m−H4⋅2.5m=020kN+H4=0V2−2⋅10kN+V4=0−20kN⋅2m+M2=0 \begin{cases} 10kN/m \cdot 2m \cdot \frac{1}{2} \cdot 2m + 30kNm - V_4 \cdot 3m - H_4 \cdot 2.5m = 0 \\\\ 20kN + H_4 = 0 \\\\ V_2 - 2 \cdot 10kN + V_4 = 0 \\\\ -20kN \cdot 2m + M_2 = 0 \end{cases}

Z kolei jeżeli napotkamy trudniejsze przypadki obliczeń możemy dokonać przy pomocy macierzy.

Suma momentów dla całej ramy (sprawdzenie):

∑MW1=0\sum M_{W1} = 0

M2−2m⋅20kN+10kN⋅2m⋅12⋅2m+30kNm+H4⋅2.5m−V4⋅3m=0M_2 - 2m \cdot 20kN + 10kN \cdot 2m \cdot \frac{1}{2} \cdot 2m + 30kNm + H_4 \cdot 2.5m - V_4 \cdot 3m = 0

40kNm−40kNm+20kNm+30kNm+50kNm−100kNm=040kNm - 40kNm + 20kNm + 30kNm + 50kNm - 100kNm = 0

0=00 = 0

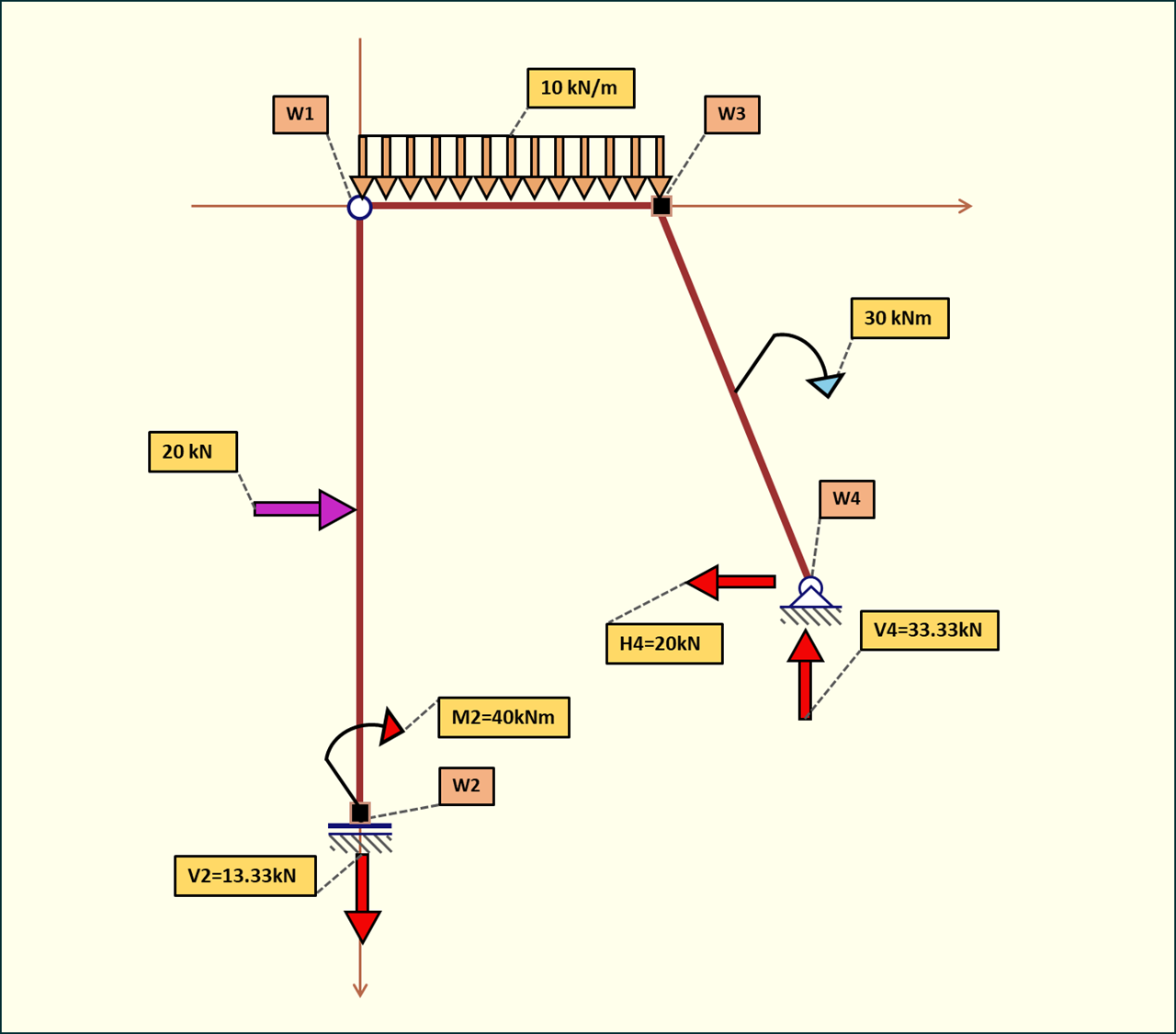
Rys. 4. Reakcje podporowe obliczone

3. Obliczanie składowych sił pod kątem na podporze w węźle W4

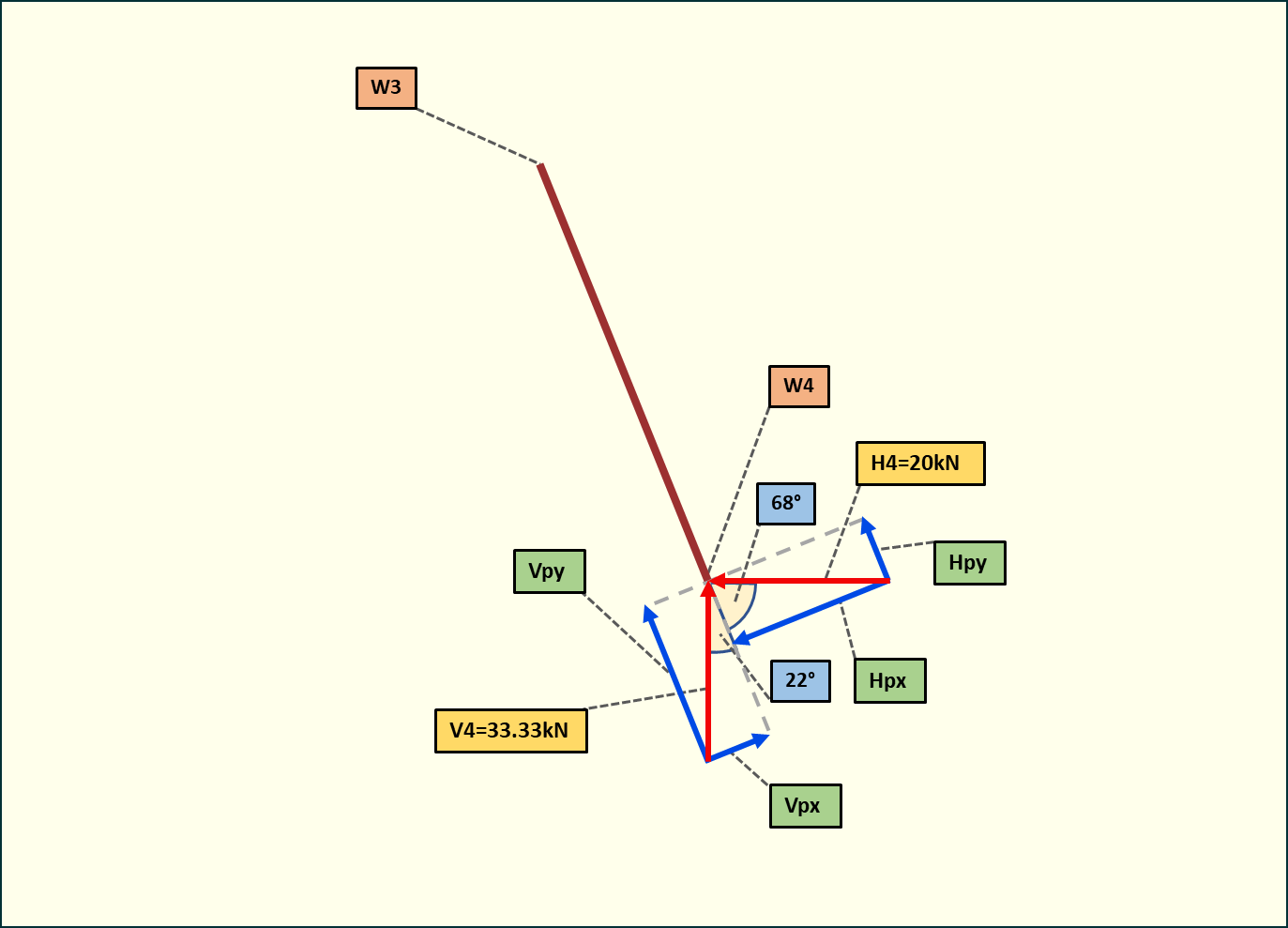
Rys. 5. Obliczenie składowych sił pod kątem na podporze w węźle W4

Vpy=33.33kN⋅cos⁡22°=30.90kNV_{py} = 33.33kN \cdot \cos 22° = 30.90kN

Vpx=33.33kN⋅sin⁡22°=12.49kNV_{px} = 33.33kN \cdot \sin 22° = 12.49kN

Hpy=20kN⋅cos⁡68°=7.49kNH_{py} = 20kN \cdot \cos 68° = 7.49kN

Hpx=20kN⋅sin⁡68°=18.54kNH_{px} = 20kN \cdot \sin 68° = 18.54kN

4. Siły wewnętrzne

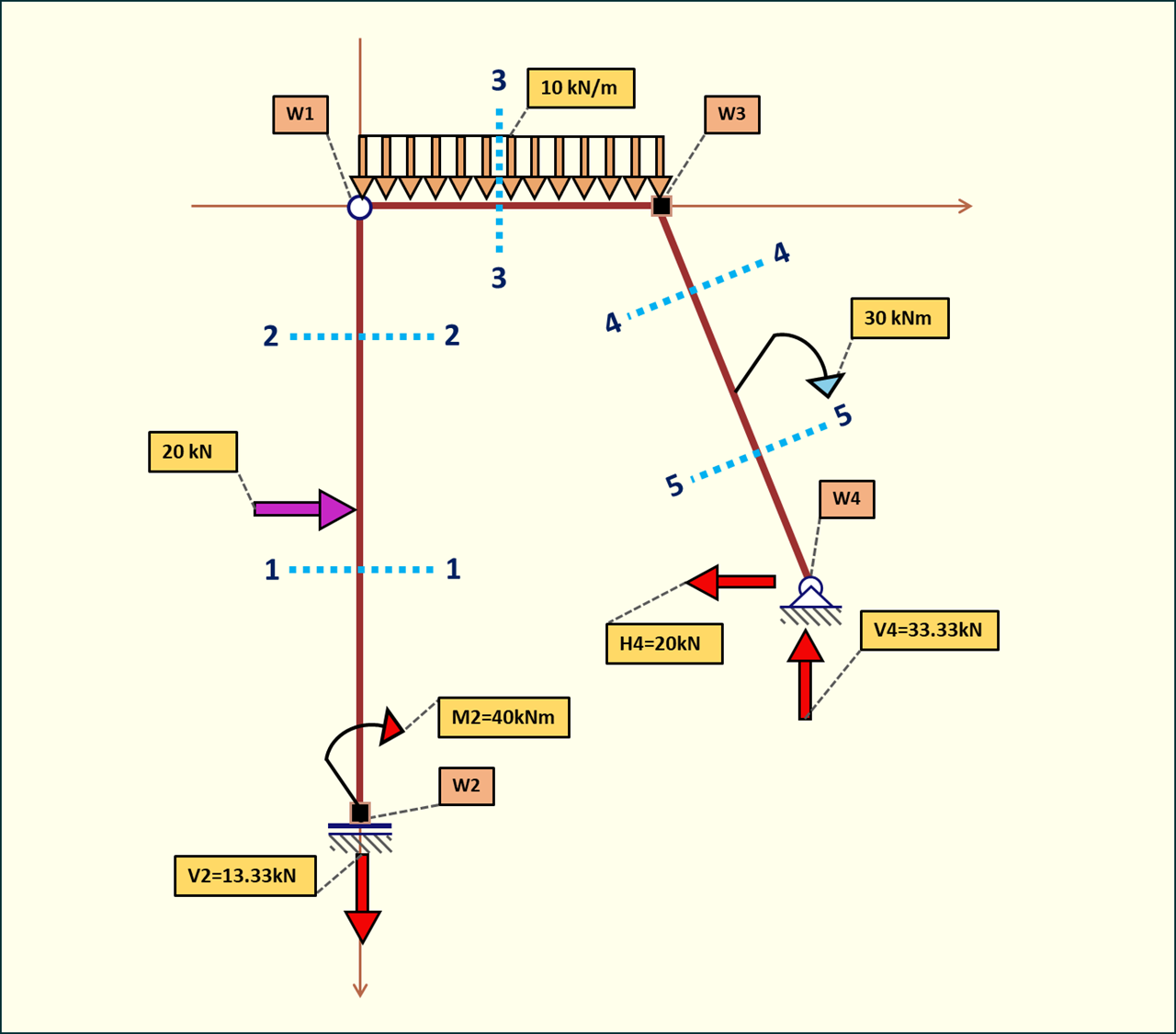
Rys. 6. Podział ramy

4.1. Siły w przegubie

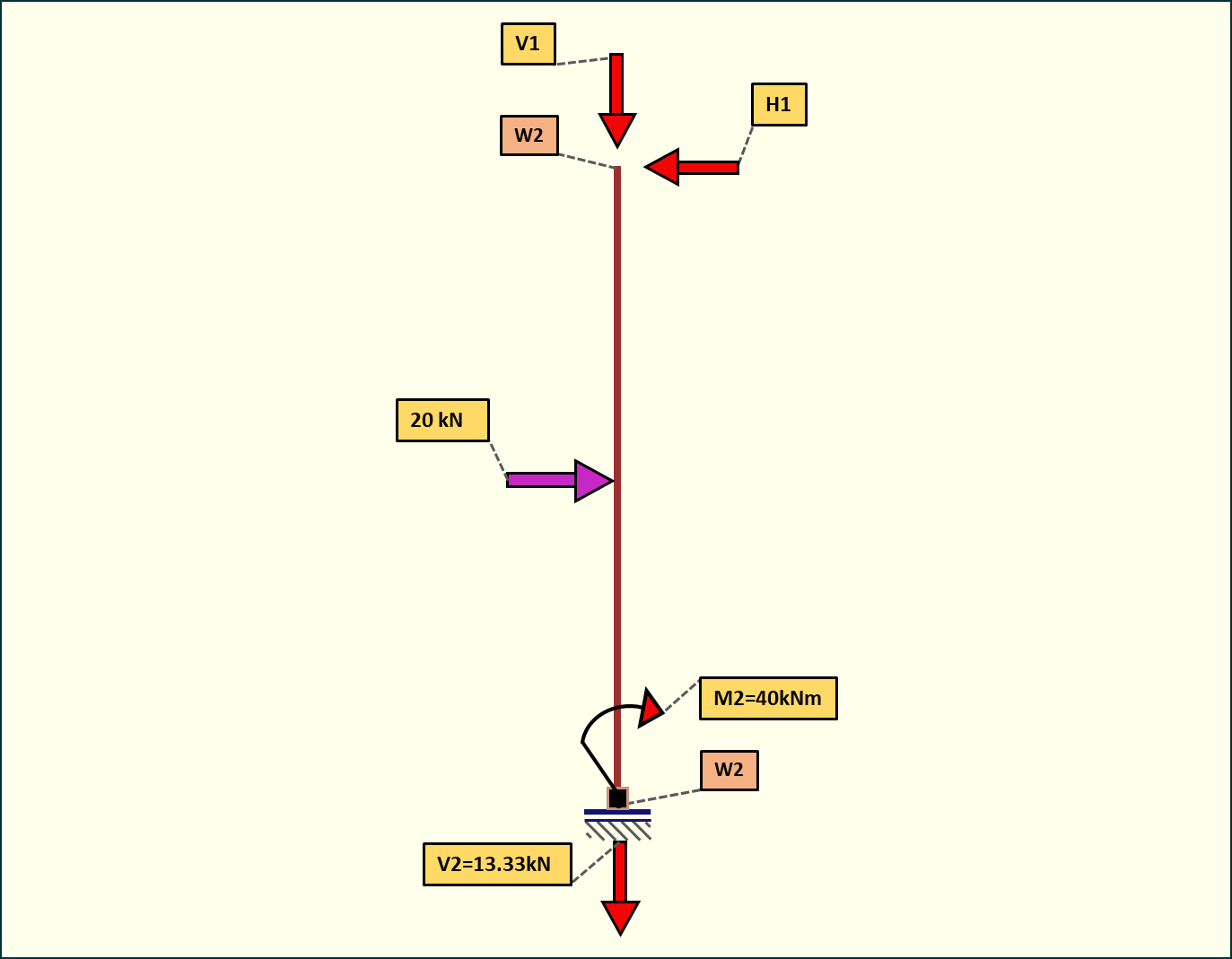
Rys. 7. Siły w przegubie

∑PY=0\sum P_Y = 0

−H1+20kN=0-H_1 + 20kN = 0

H1=20kNH_1 = 20kN
∑PX=0\sum P_X = 0

13.33kN+V1=013.33kN + V_1 = 0

V1=−13.33kNV_1 = -13.33kN
4.2. Siły tnące

Przedział 1-1

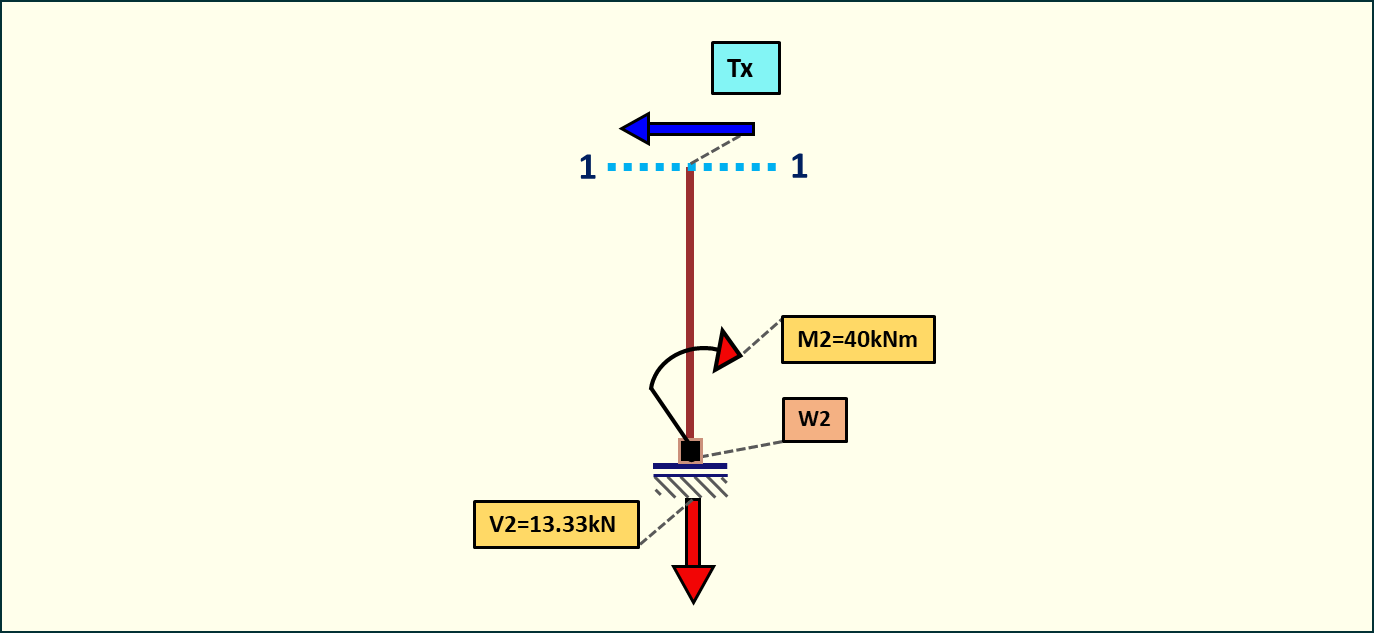
Rys. 8. Siły tnące w przedziale 1-1

∑PY=0\sum P_Y = 0

Tx=0T_x = 0

Siła tnąca w punkcie 1 będzie równa 0, ponieważ nie występuje reakcja podporowa poprzeczna.

Przedział 2-2

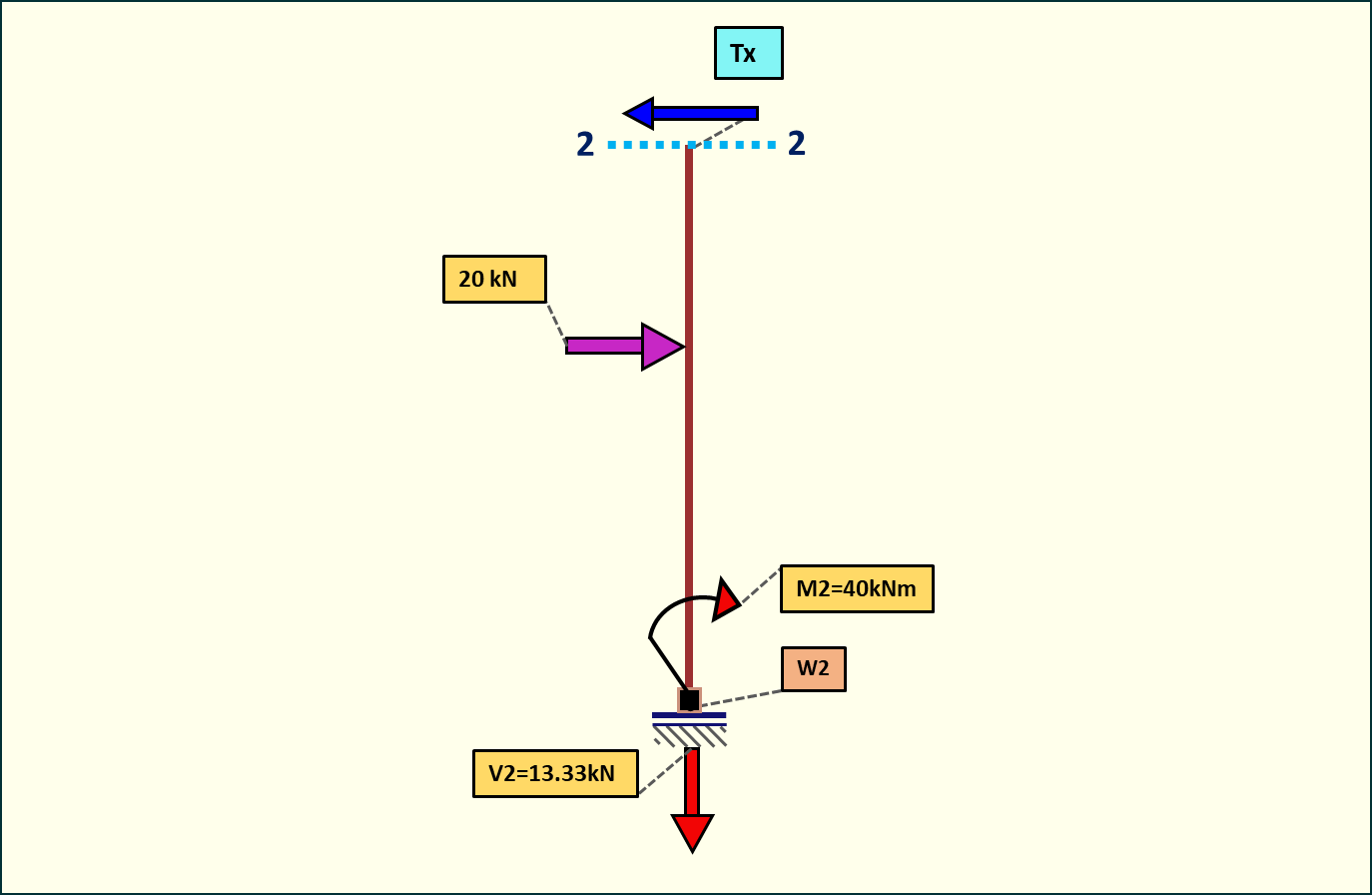
Rys. 9. Siły tnące w przedziale 2-2

∑PY=0\sum P_Y = 0

−TX+20kN=0-T_X + 20kN = 0

TX=20kNT_X = 20kN

W punkcie nr 2 występuje skok o 20kN, więc TX=20kNT_X=20kN

Przedział 3-3 0 <= x <= 2

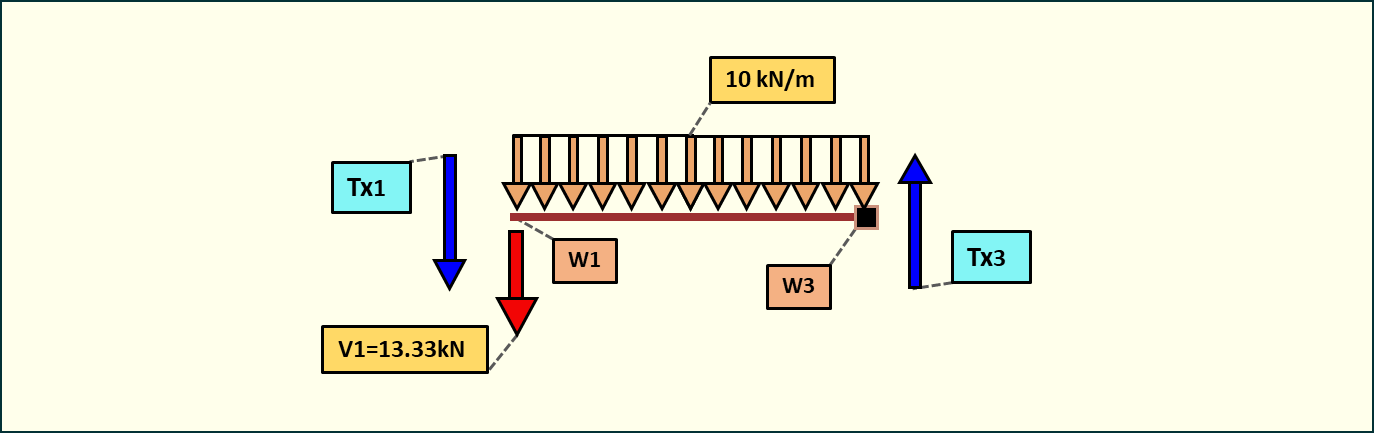
Rys. 10. Siły tnące w przedziale 3-3

∑Pxw1=0\sum P_{xw1} = 0

TX1−13.33=0T_{X1} - 13.33 = 0

TX1=13.33kNT_{X1} = 13.33kN

∑Pxw3=0\sum P_{xw3} = 0

−TX3+13.33+10⋅x⋅12x=0-T_{X3} + 13.33 + 10 \cdot x \cdot \frac{1}{2}x = 0

TX3=13.33+5x2T_{X3} = 13.33 + 5x^2

TX3=13.33+5⋅22=33.33kNT_{X3} = 13.33 + 5 \cdot 2^2 = 33.33kN

W węźle nr 1 wartość tnącej będzie równa równoległej reakcji podporowej.

W węźle nr 3 wartość tnącej będzie równa sumie wartości z węzła nr 1 i wypadkowej z obciążenia. Siły z tych samych zwrotów.

Przedział 5-5

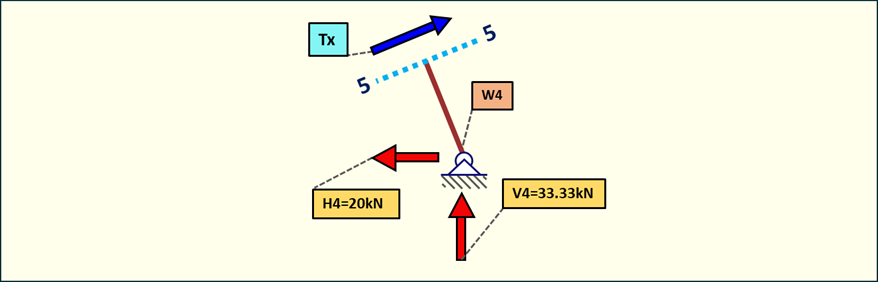
Rys. 11. Siły tnące w przedziale 5-5

∑Py=0\sum P_y = 0

TX+20kN⋅sin⁡68°−33.33⋅sin⁡22°=0T_X + 20kN \cdot \sin 68° - 33.33 \cdot \sin 22° = 0

TX=6.05kNT_X = 6.05kN

W punkcie nr W4 wartość będzie równa rożnicy sumy rzutów na oś „x" reakcji podporowych. Siły są równych zwrotów. Na pręcie 4-5 nie występuje żadna zmiana wartości sił tnących.

TX=HPX−HPY=18.54kN−12.49kN=6.05kNT_X = H_{PX} - H_{PY} = 18.54kN - 12.49kN = 6.05kN

Przedział 4-4

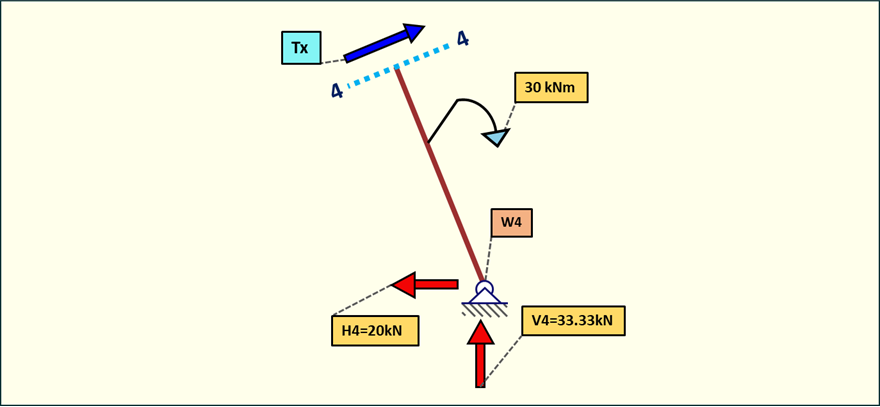
Rys. 12. Siły tnące w przedziale 4-4

To samo co w przedziale 5-5. Żadna siła nie dochodzi.

Rys. 13. Wykres sił tnących

4.3. Siły normalne

Siły normalne możemy liczyć analogicznie do sił tnących, ale uwzględniamy tylko siły podłużne.

Przedział 1-1

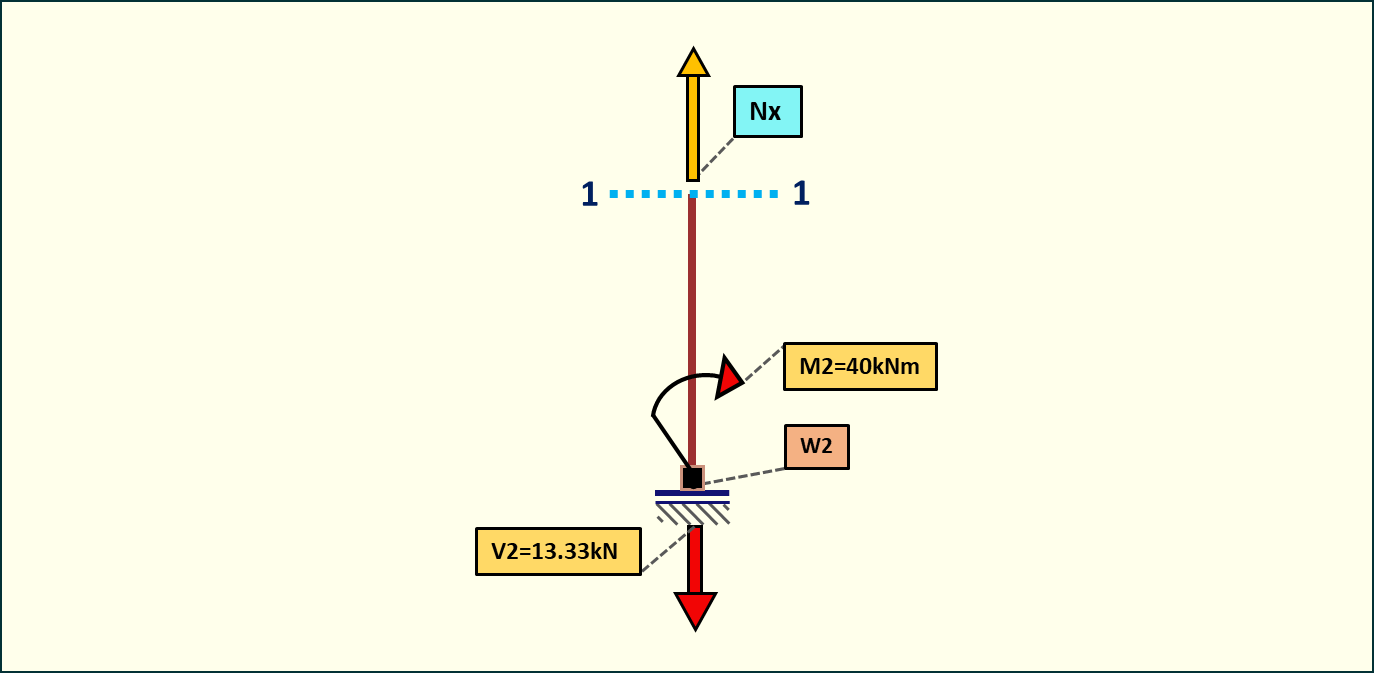
Rys. 14. Siły normalne w przedziale 1-1

Wzdłuż pręta 1-2 działa reakcja podporowa.

∑Px=0\sum P_x = 0

−NX+13.33=0-N_X + 13.33 = 0

NX=13.33kNN_X = 13.33kN

Przedział 2-2

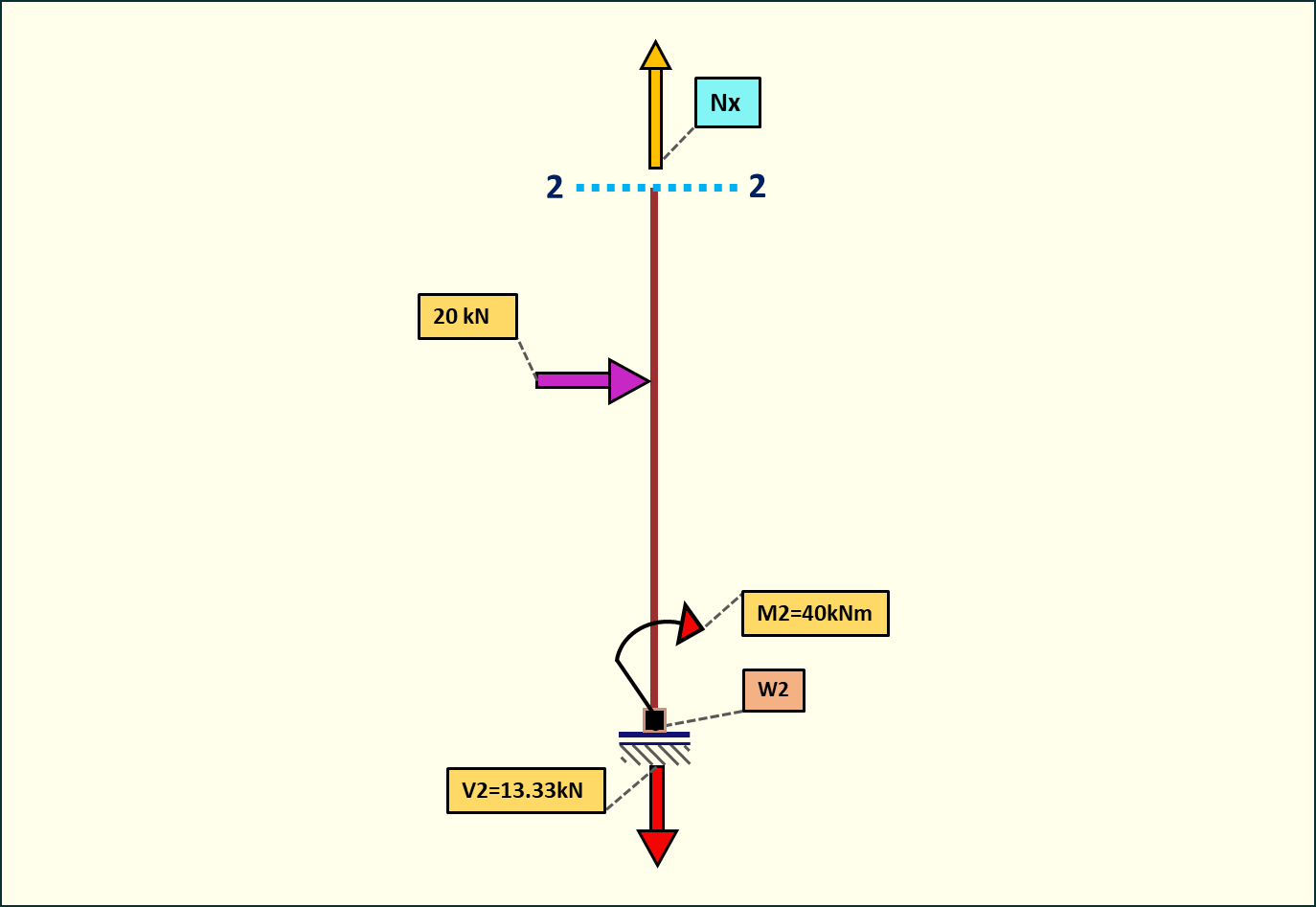
Rys. 15. Siły normalne w przedziale 2-2

∑Px=0\sum P_x = 0

−NX+13.33=0-N_X + 13.33 = 0

NX=13.33kNN_X = 13.33kN

Przedział 3-3

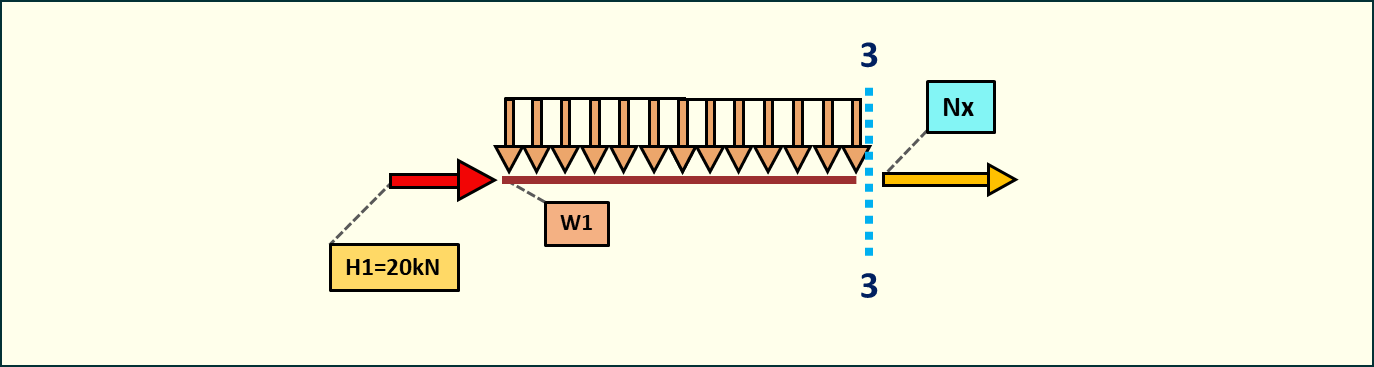
Rys. 16. Siły normalne w przedziale 3-3

Wzdłuż pręta 1-3 działa siła podłużna 20kN.

∑Py=0\sum P_y = 0

NX+20=0N_X + 20 = 0

NX=−20kNN_X = -20kN

Przedział 5-5

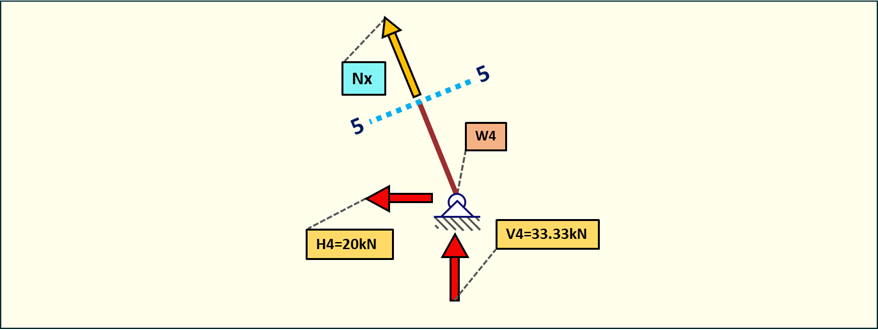
Rys. 17. Siły normalne w przedziale 5-5

∑Px=0\sum P_x = 0

−20kN⋅cos⁡68°−33.33⋅cos⁡22°−NX=0-20kN \cdot \cos 68° - 33.33 \cdot \cos 22° - N_X = 0

NX=−38.39kNN_X = -38.39kN

Przedział 4-4

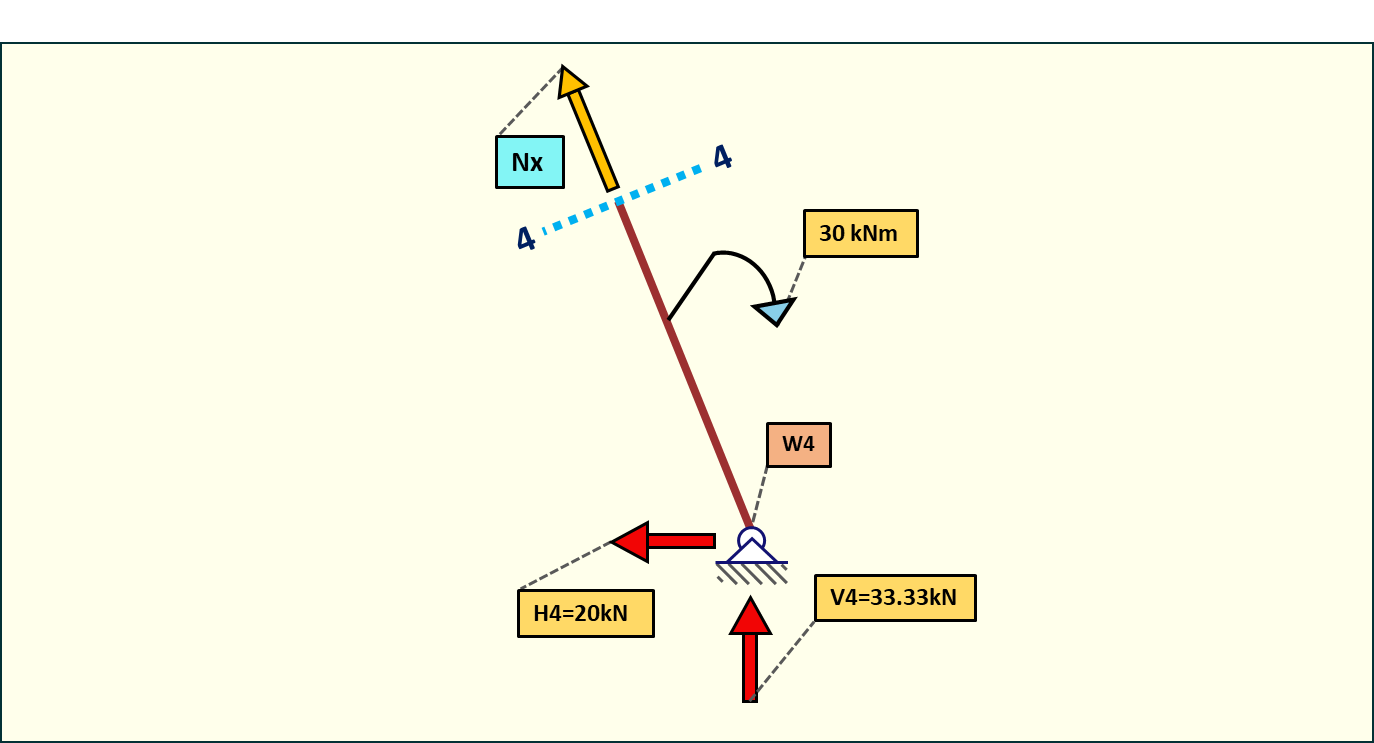
Rys. 18. Siły normalne w przedziale 4-4

Wzdłuż pręta 3-4 działają siły podłużne pochodzące od reakcji podporowych. Obie siły ściskają pręt.

∑Py=0\sum P_y = 0

−20kN⋅cos⁡68°−33.33⋅cos⁡22°−NX=0-20kN \cdot \cos 68° - 33.33 \cdot \cos 22° - N_X = 0

NX=−38.39kNN_X = -38.39kN

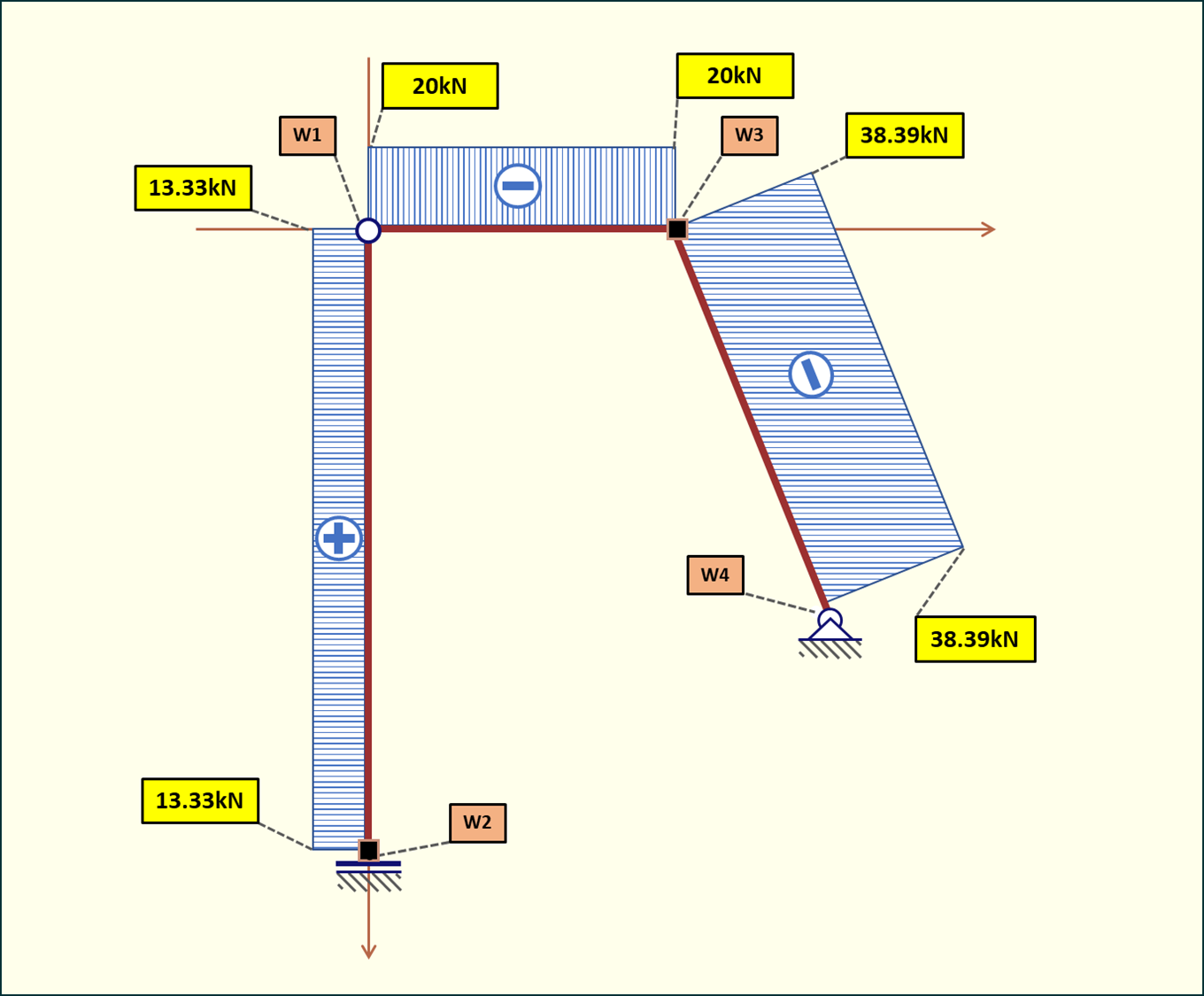
Rys. 19. Wykres sił normalnych

4.4. Momenty zginające

Wykresy momentów najprościej jest policzyć licząć wartości tych wykresów w punktach przyłożenia siły. Uwzględniamy siły poprzeczne i momenty skupione. Siły podłużne nie dają wartości momentów, ponieważ ich ramię wynosi 0. Zaczynamy od podpór.

Przedział 1-1

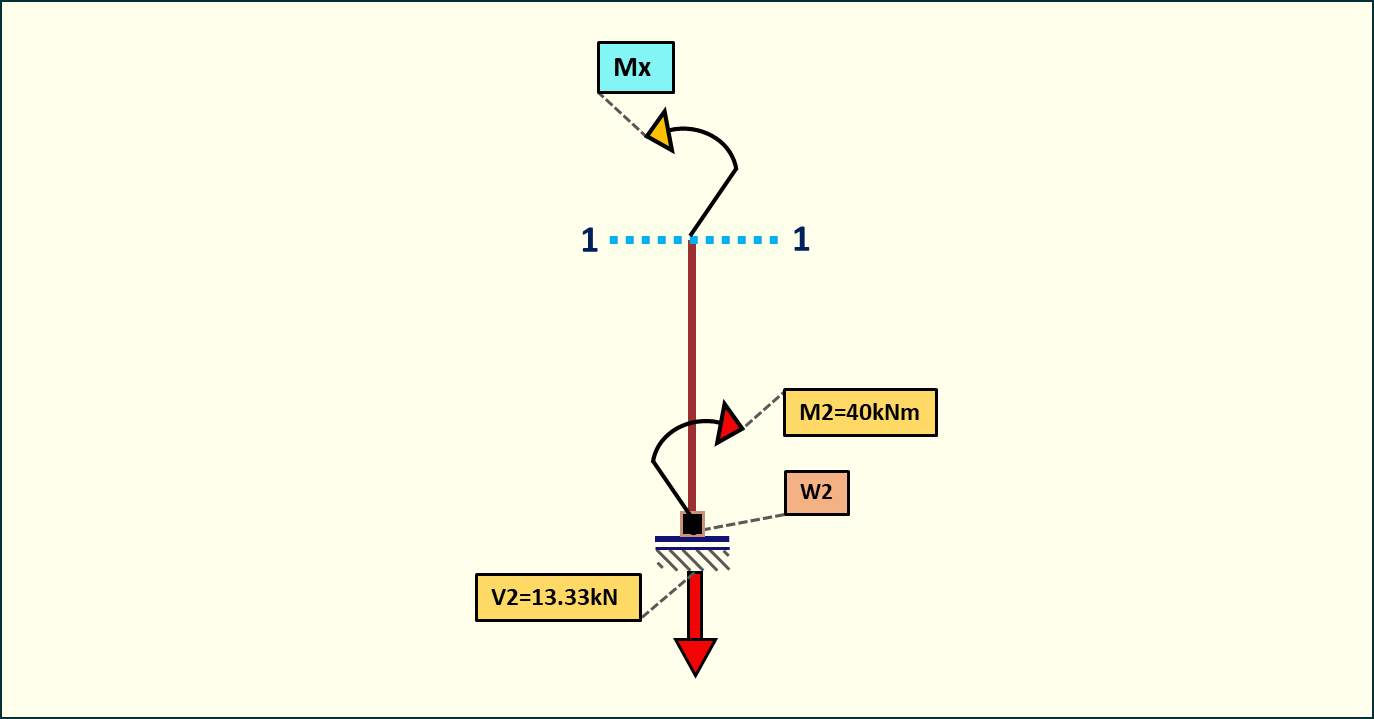
Rys. 20. Momenty zginające w przedziale 1-1

Moment w tym przedziale będzie równy momentowi na podporze.

∑M=0\sum M = 0

−MX+40kNm=0-M_X + 40kNm = 0

MX=40kNmM_X = 40kNm

Przedział 2-2 0 <= x <= 2

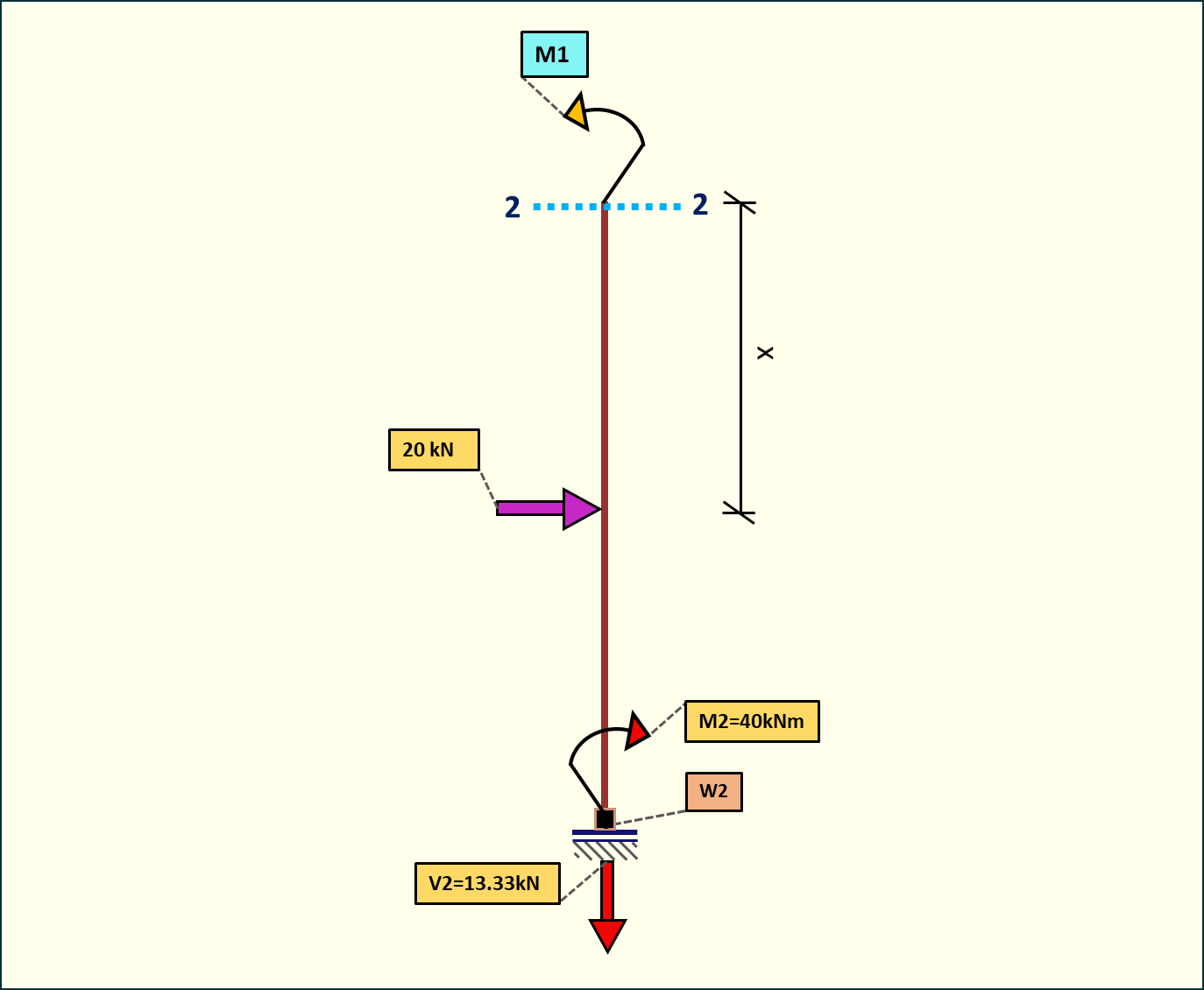
Rys. 21. Momenty zginające w przedziale 2-2

∑M=0\sum M = 0

−MX+40kNm−20kN⋅x=0-M_X + 40kNm - 20kN \cdot x = 0

MX=40kNm−20kN⋅xM_X = 40kNm - 20kN \cdot x

M2=40kNm−20kN⋅0=40kNmM_2 = 40kNm - 20kN \cdot 0 = 40kNm

M1=40kN−20kN⋅2m=0kNmM_1 = 40kN - 20kN \cdot 2m = 0kNm

Od punktu, w którym znajduje się siła 20kN moment będzie liniowo malał, ponieważ skraca się długość ramienia na jakim działa siła.

Przedział 3-3

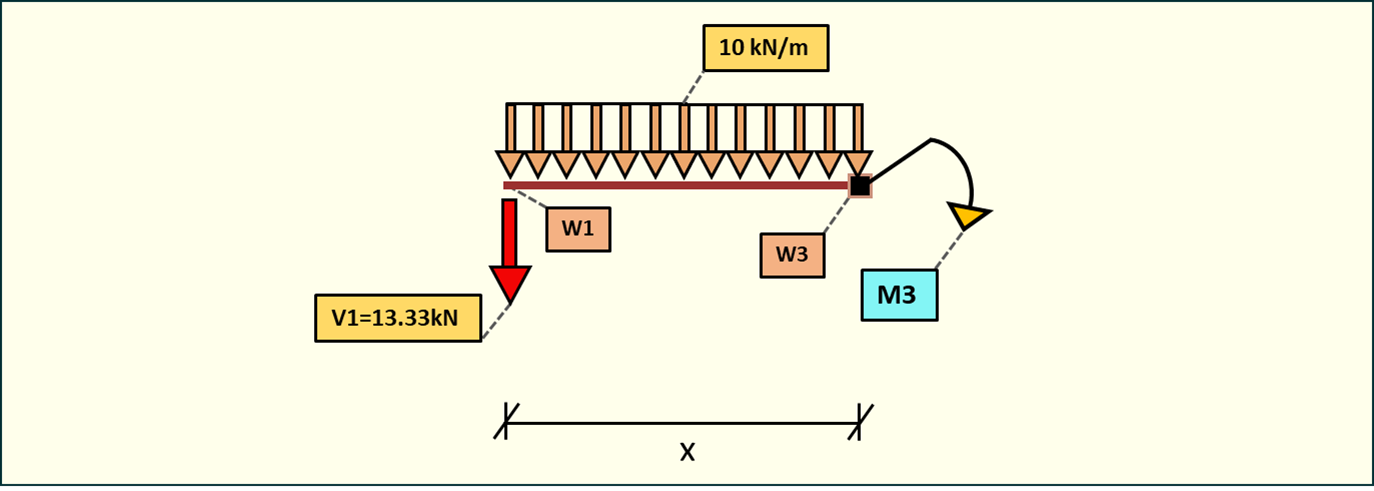
Rys. 22. Momenty zginające w przedziale 3-3

Moment w przegubie jest zawsze równy 0 (węzeł nr 1).

∑M=0\sum M = 0

MX−13.33kN⋅x−10kNm⋅x⋅12⋅x=0M_X - 13.33kN \cdot x - \frac{10kN}{m} \cdot x \cdot \frac{1}{2} \cdot x = 0

MX=13.33kN⋅x+5x2M_X = 13.33kN \cdot x + 5x^2

MX=13.33kN⋅2m+5⋅22=26.66kNm+20kNm=46.66kNmM_X = 13.33kN \cdot 2m + 5 \cdot 2^2 = 26.66kNm + 20kNm = 46.66kNm

Przedział 5-5

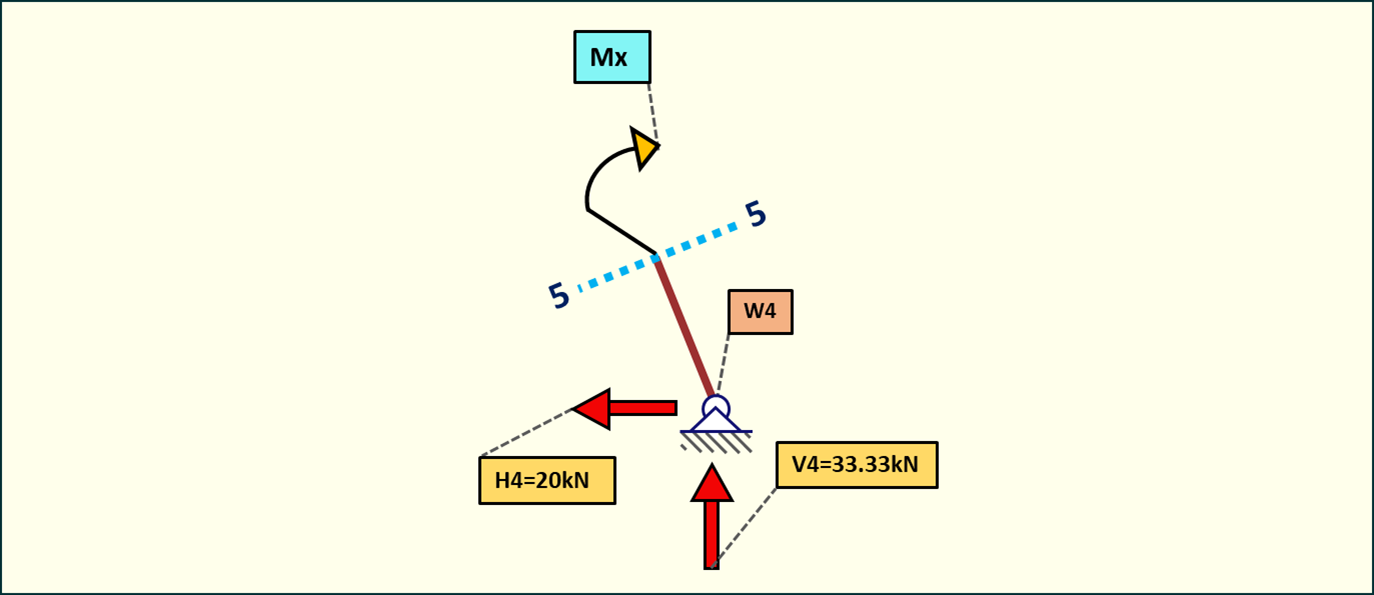
Rys. 23. Momenty zginające w przedziale 5-5

Moment na podporze jest równy 0 (węzeł nr 4).

Mx=0Mx = 0

Przedział 4-4

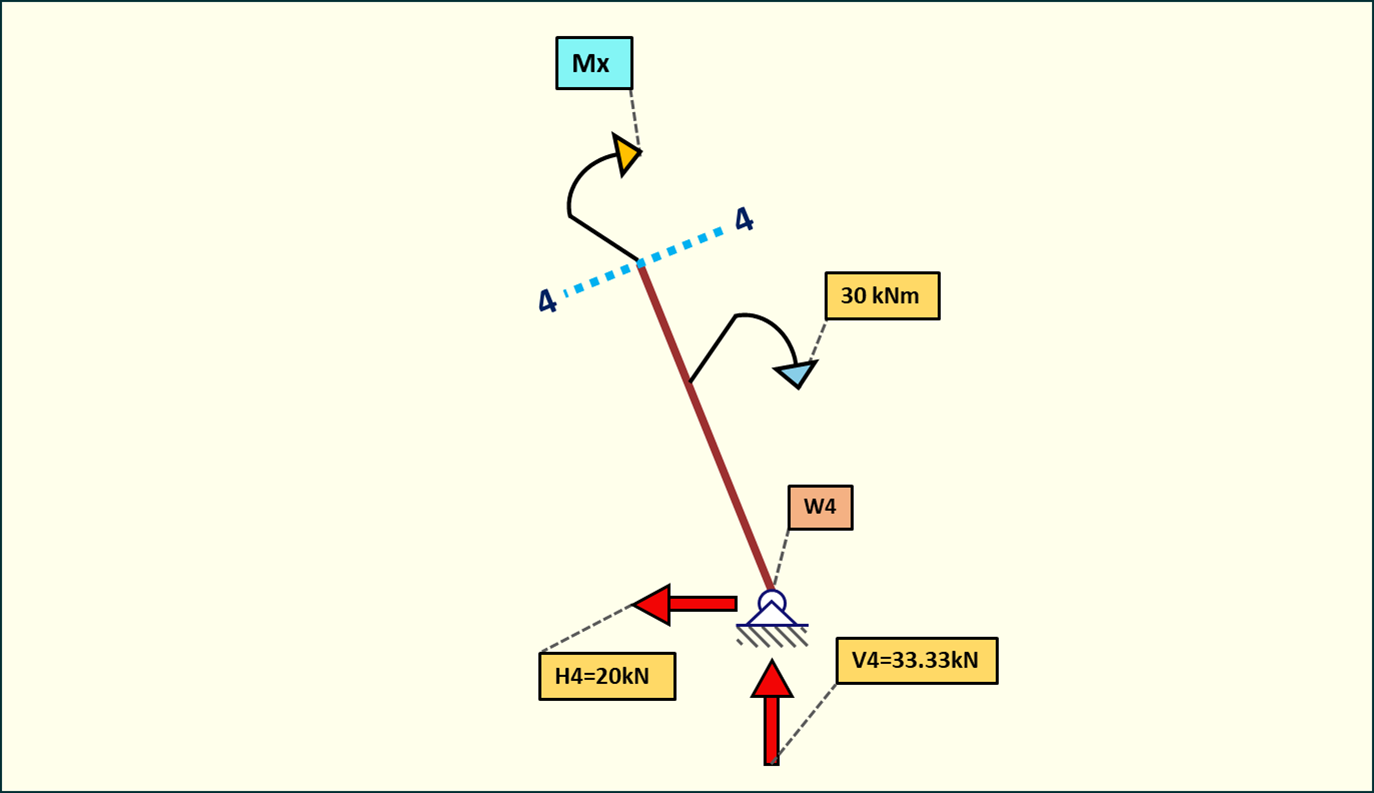
Rys. 24. Momenty zginające w przedziale 4-4

Moment na środku pręta w3-4 będzie pochodził od składowych reakcji podporowych.

∑M=0\sum M = 0

MX=−VPX⋅1.35m+HPX⋅1.35mM_X = -V_{PX} \cdot 1.35m + H_{PX} \cdot 1.35m

Mx=−12.49kN⋅1.35m+18.54kN⋅1.35m=8.17kNmM_x = -12.49kN \cdot 1.35m + 18.54kN \cdot 1.35m = 8.17kNm

Występuje tutaj także skok momentu o 30kNm.

MX+30kNm=38.17kNmM_X + 30kNm = 38.17kNm

Moment w węźle nr 3 będzie pochodził od składowych reakcji podporowych na odpowiednim ramieniu oraz momentowi przyłożonemu.

∑M1−1=0\sum M_{1-1} = 0

MX=30kN+HPX⋅2.7m−VPX⋅1.35mM_X = 30kN + H_{PX} \cdot 2.7m - V_{PX} \cdot 1.35m

MX=30kN+18.54kN⋅2.7m−12.49kN⋅2.7m=46.34kNmM_X = 30kN + 18.54kN \cdot 2.7m - 12.49kN \cdot 2.7m = 46.34kNm

Od węzła nr 3 momenty będą maleć do podpory, gdzie ich wartość będzie zerowa. Wykres będzie malejącą funkcją kwadratową ze względu na rodzaj obciążenia.

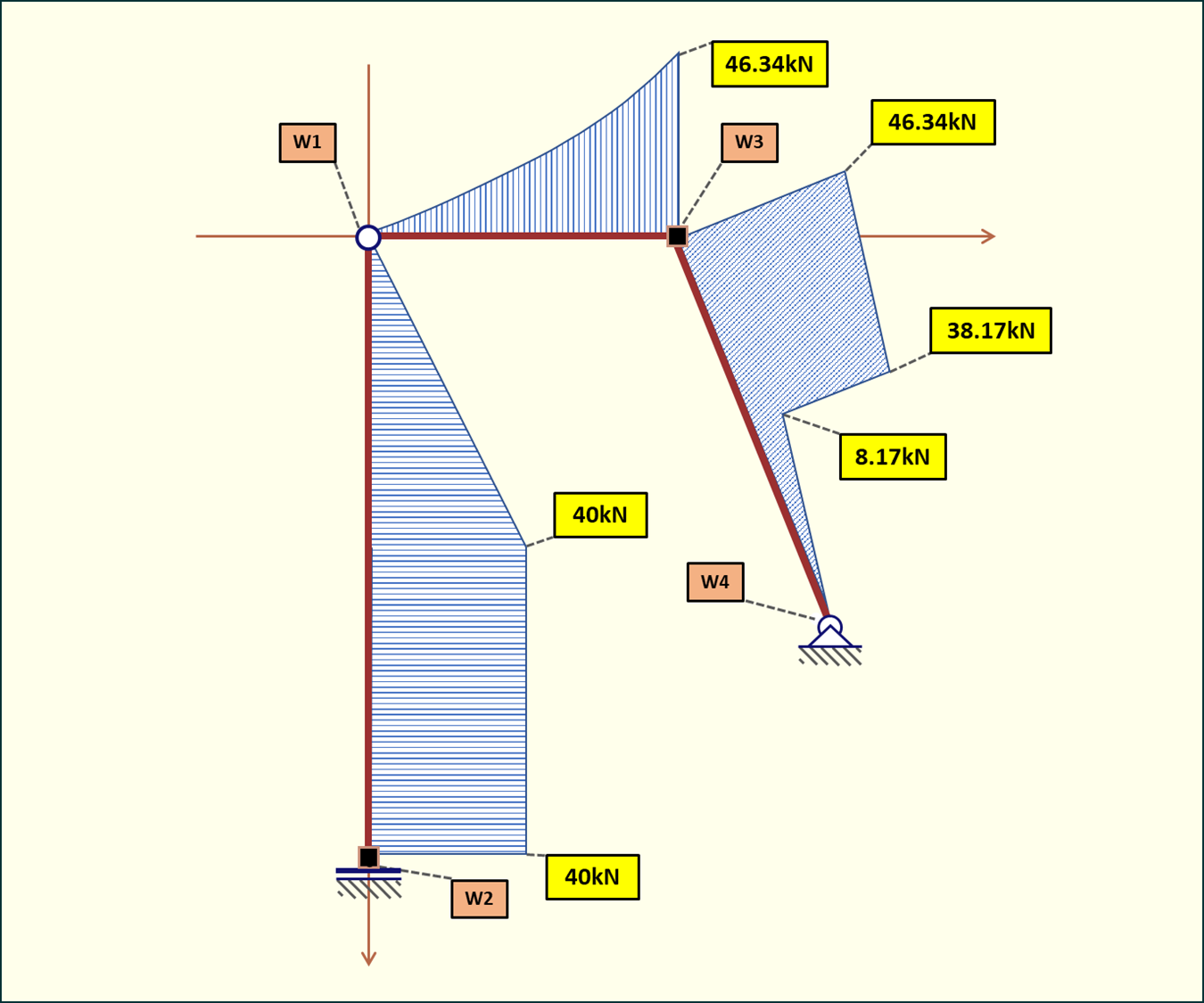
Rys. 25. Wykres momentów zginających

Ostatnia aktualizacja:
Belka statycznie wyznaczalna - przykład krok po krokuIdentyfikacja prętów zerowych kratownicy