Kącik Wiedzy
Momenty bezwładności - przykład nr 1

Momenty bezwładności - przykład nr 1

września 30, 2018

Wprowadzenie

Zadanie: Wyznaczyć położenie głównych centralnych osi bezwładności i obliczyć główne centralne momenty bezwładności.

1. Schemat zadania

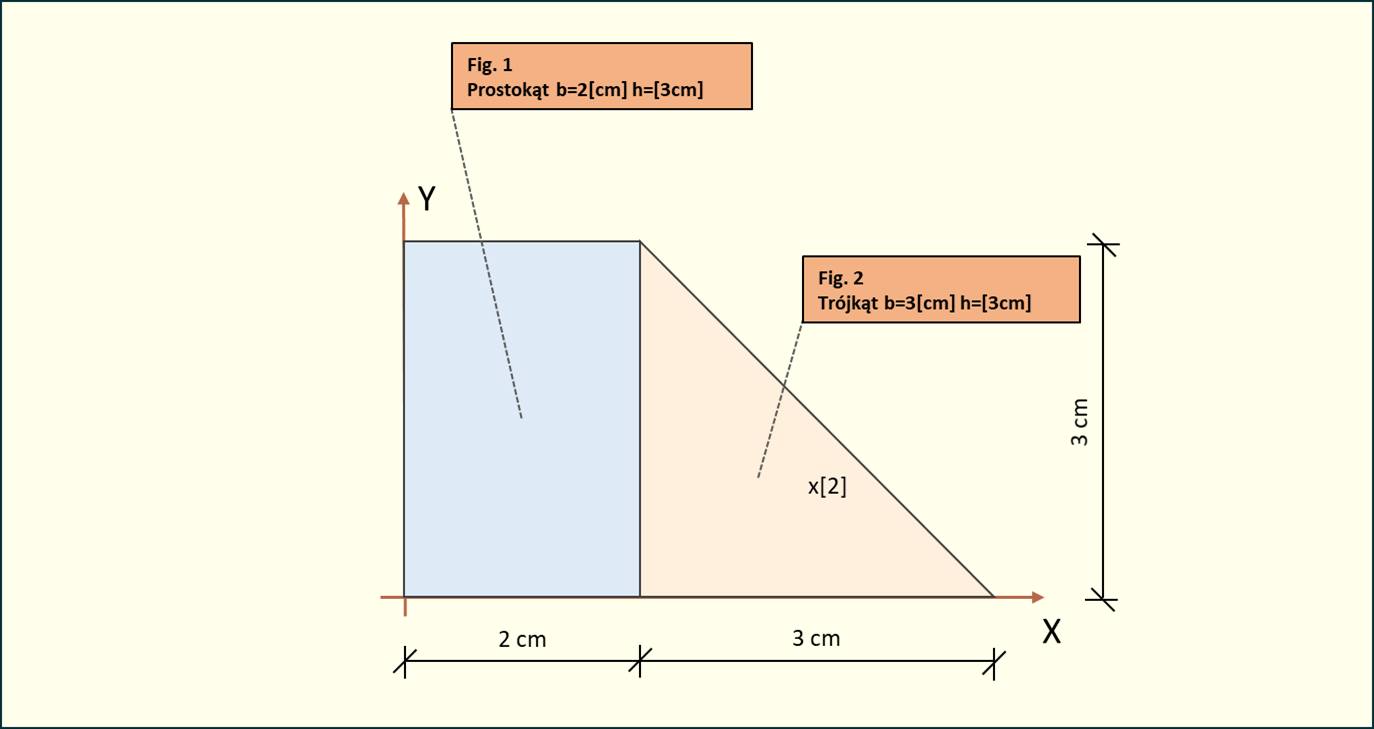
Rys. 1. Schemat zadania

2. Charakterystyki geometryczne poszczególnych figur układu

2.1 Figura nr 1

Prostokąt:

  • b=2cmb=2 cm
  • h=3cmh=3 cm
  • kąt OX:0OX: 0 stopni

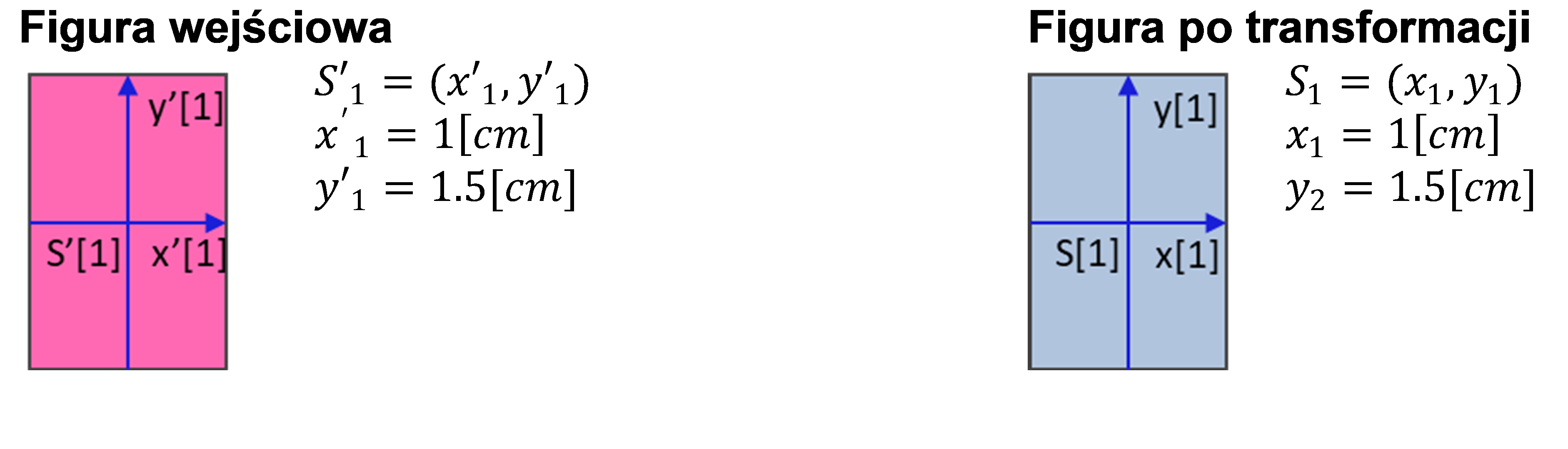
Rys. 2. Figura nr 1 - przed i po transformacji

Transformacja liniowa figury do punktu docelowego o wektor dXdX i dYdY:

dX=0 cmdX = 0\ cmdY=0 cmdY = 0\ cmx1=0+b2=0+2 cm2=1 cmx_1 = 0 + \frac{b}{2} = 0 + \frac{2\ cm}{2} = 1\ cmy1=0+h2=0+3 cm2=1,5 cmy_1 = 0 + \frac{h}{2} = 0 + \frac{3\ cm}{2} = 1{,}5\ cmA1=b⋅h=2 cm⋅3 cm=6 cm2A_1 = b \cdot h = 2\ cm \cdot 3\ cm = 6\ cm^2S1=(x1;y1)S_1 = (x_1; y_1)Sx1=A1⋅y1=6 cm2⋅1,5 cm=9 cm3Sx_1 = A_1 \cdot y_1 = 6\ cm^2 \cdot 1{,}5\ cm = 9\ cm^3Sy1=A1⋅x1=6 cm2⋅1 cm=6 cm3Sy_1 = A_1 \cdot x_1 = 6\ cm^2 \cdot 1\ cm = 6\ cm^3Jx1=b⋅h312=2⋅3312=54 cm412=4,5 cm4Jx_1 = \frac{b \cdot h^3}{12} = \frac{2 \cdot 3^3}{12} = \frac{54\ cm^4}{12} = 4{,}5\ cm^4Jy1=b3⋅h12=23⋅312=24 cm412=2 cm4Jy_1 = \frac{b^3 \cdot h}{12} = \frac{2^3 \cdot 3}{12} = \frac{24\ cm^4}{12} = 2\ cm^4Dxy1=0Dxy_1 = 0
2.2 Figura nr 2

Trójkąt:

  • b=3 cmb=3\ cm
  • h=3 cmh=3\ cm
  • kąt OX:0OX: 0 stopni

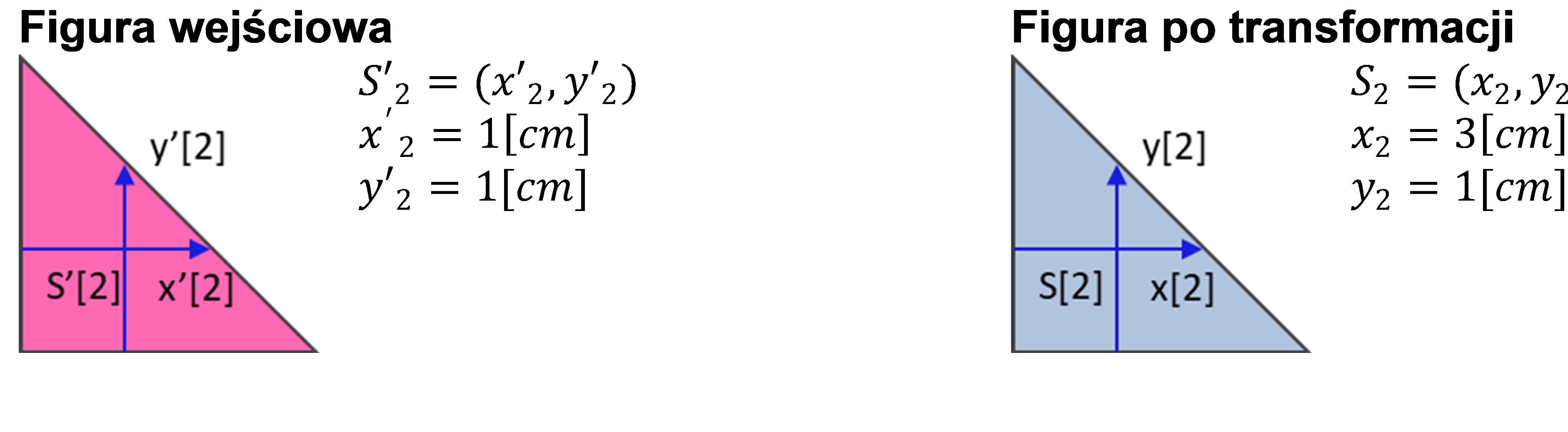
Rys. 3. Figura nr 2 - przed i po transformacji

Transformacja liniowa figury do punktu docelowego o wektor dXdX i dYdY:

dX=2 cmdX = 2\ cmdY=0 cmdY = 0\ cmx2=2 cm+b3=2 cm+3 cm3=3 cmx_2 = 2\ cm + \frac{b}{3} = 2\ cm + \frac{3\ cm}{3} = 3\ cmy2=0+h3=0+3 cm3=1 cmy_2 = 0 + \frac{h}{3} = 0 + \frac{3\ cm}{3} = 1\ cmA2=12⋅b⋅h=12⋅3 cm⋅3 cm=4,5 cm2A_2 = \frac{1}{2} \cdot b \cdot h = \frac{1}{2} \cdot 3\ cm \cdot 3\ cm = 4{,}5\ cm^2S2=(x2;y2)S_2 = (x_2; y_2)Sx2=A2⋅y2=4,5 cm2⋅1 cm=4,5 cm3Sx_2 = A_2 \cdot y_2 = 4{,}5\ cm^2 \cdot 1\ cm = 4{,}5\ cm^3Sy2=A2⋅x2=4,5 cm2⋅3 cm=13,5 cm3Sy_2 = A_2 \cdot x_2 = 4{,}5\ cm^2 \cdot 3\ cm = 13{,}5\ cm^3Jx2=b⋅h336=3⋅3336=81 cm436=2,25 cm4Jx_2 = \frac{b \cdot h^3}{36} = \frac{3 \cdot 3^3}{36} = \frac{81\ cm^4}{36} = 2{,}25\ cm^4Jy2=b3⋅h36=33⋅336=81 cm436=2,25 cm4Jy_2 = \frac{b^3 \cdot h}{36} = \frac{3^3 \cdot 3}{36} = \frac{81\ cm^4}{36} = 2{,}25\ cm^4Dxy2=−b2⋅h272=−32⋅3272=−81 cm472=−1,125 cm4Dxy_2 = -\frac{b^2 \cdot h^2}{72} = -\frac{3^2 \cdot 3^2}{72} = -\frac{81\ cm^4}{72} = -1{,}125\ cm^4

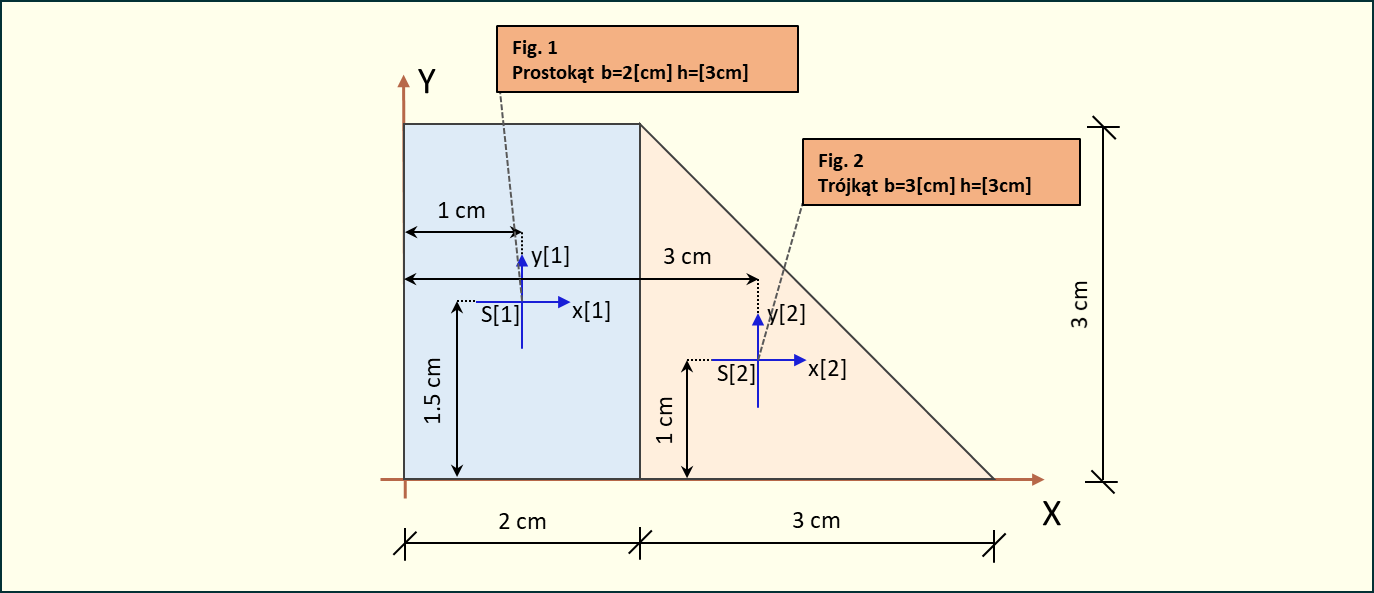
Rys. 4. Układ figur z zaznaczonymi środkami ciężkości

3. Położenie głównych centralnych osi bezwładności (xc, yc) względem układu XY

Dla ułatwienia obliczeń zestawimy wszystkie dane w formie tabelarycznej:

Tab. 1. Zestawienie charakterystyk poszczególnych figur

Mając powyższe dane możemy obliczyć geometryczny środek układu figur płaskich:

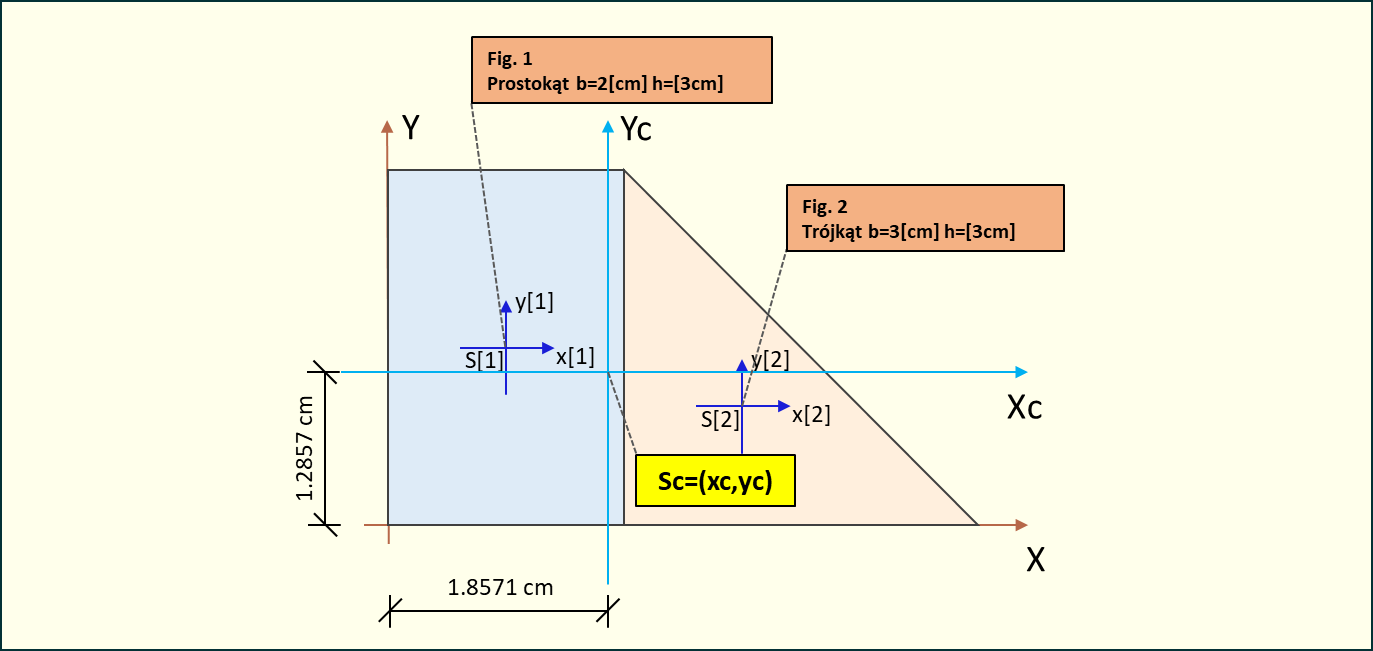
xc=∑Syi∑Ai=Sy1+Sy2A1+A2=6 cm3+13,5 cm36 cm2+4,5 cm2=19,5 cm310,5 cm2≈1,8571 cmx_c = \frac{\sum Sy_i}{\sum A_i} = \frac{Sy_1 + Sy_2}{A_1 + A_2} = \frac{6\ cm^3 + 13{,}5\ cm^3}{6\ cm^2 + 4{,}5\ cm^2} = \frac{19{,}5\ cm^3}{10{,}5\ cm^2} \approx 1{,}8571\ cmyc=∑Sxi∑Ai=Sx1+Sx2A1+A2=9 cm3+4,5 cm36 cm2+4,5 cm2=13,5 cm310,5 cm2≈1,2857 cmy_c = \frac{\sum Sx_i}{\sum A_i} = \frac{Sx_1 + Sx_2}{A_1 + A_2} = \frac{9\ cm^3 + 4{,}5\ cm^3}{6\ cm^2 + 4{,}5\ cm^2} = \frac{13{,}5\ cm^3}{10{,}5\ cm^2} \approx 1{,}2857\ cm

Rys. 5. Geometryczny środek układu figur płaskich

4. Odległości od środka ciężkości figury do środka ciężkości układu

Mając wszystkie potrzebne dane możemy zatem obliczyć odległości między środkami ciężkości poszczególnych figur a środkiem ciężkości całego układu:

xci=xi−xcx_{ci} = x_i - x_cyci=yi−ycy_{ci} = y_i - y_c
4.1 Figura 1
xc1=x1−xc=1 cm−1,8571 cm=−0,8571 cmx_{c1} = x_1 - x_c = 1\ cm - 1{,}8571\ cm = -0{,}8571\ cmyc1=y1−yc=1,5 cm−1,2857 cm=0,2143 cmy_{c1} = y_1 - y_c = 1{,}5\ cm - 1{,}2857\ cm = 0{,}2143\ cm
4.2 Figura 2
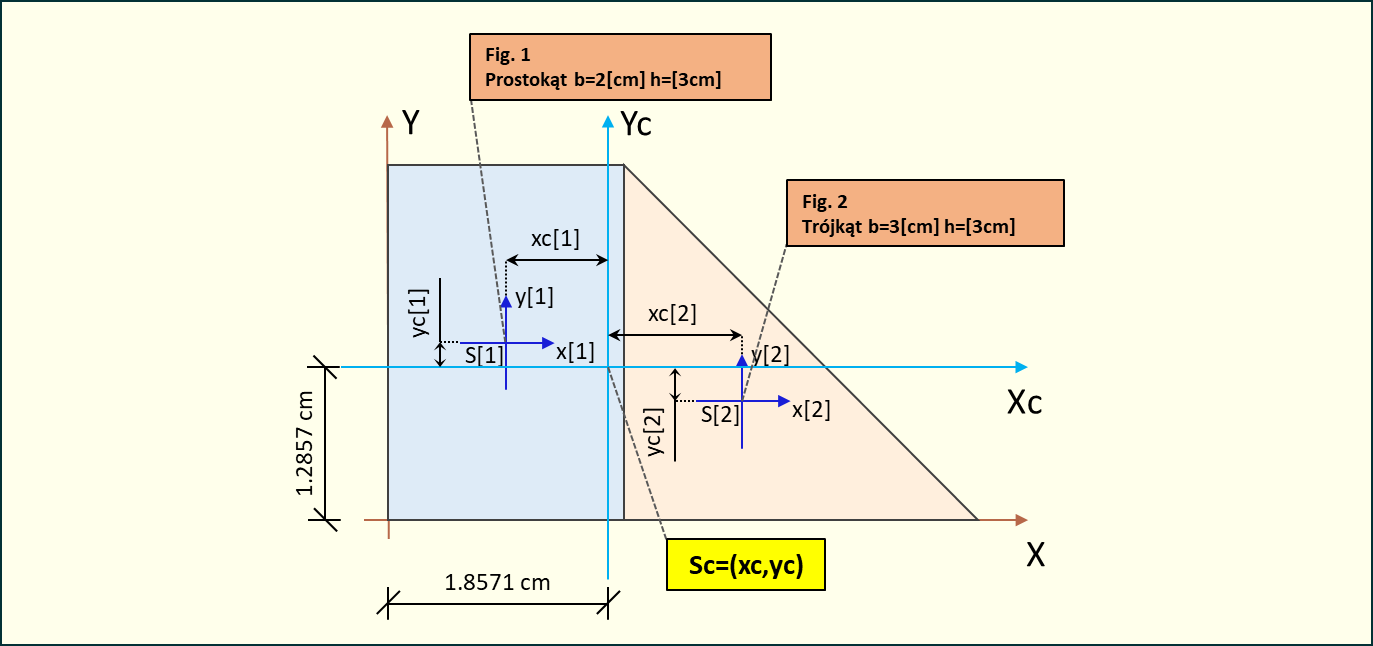
xc2=x2−xc=3 cm−1,8571 cm=1,1429 cmx_{c2} = x_2 - x_c = 3\ cm - 1{,}8571\ cm = 1{,}1429\ cmyc2=y2−yc=1 cm−1,2857 cm=−0,2857 cmy_{c2} = y_2 - y_c = 1\ cm - 1{,}2857\ cm = -0{,}2857\ cm

Rys. 5. Odległości od środka ciężkości figury do środka ciężkości układu

5. Centralne momenty bezwładności dla układu XcYc

Ponownie dla ułatwienia obliczeń zestawimy wszystkie dane w formie tabelarycznej:

Tab. 2. Zestawienie danych do obliczenia centralnych momentów bezwładności

5.1 Sumy częściowe
∑Jxi=6,75 cm4\sum Jx_i = 6{,}75\ cm^4∑Jyi=4,25 cm4\sum Jy_i = 4{,}25\ cm^4∑Dxyi=−1,125 cm4\sum Dxy_i = -1{,}125\ cm^4
5.2 Elementy do wzoru Steinera
∑Aixci2=10,2857 cm4\sum A_i x_{ci}^2 = 10{,}2857\ cm^4∑Aiyci2=0,6429 cm4\sum A_i y_{ci}^2 = 0{,}6429\ cm^4∑Aixciyci=−2,5714 cm4\sum A_i x_{ci} y_{ci} = -2{,}5714\ cm^4

6. Momenty bezwładności całego układu (twierdzenie Steinera)

Jxc=∑Jxi+∑Aiyci2=6,75+0,6429=7,3929 cm4Jx_c = \sum Jx_i + \sum A_i y_{ci}^2 = 6{,}75 + 0{,}6429 = 7{,}3929\ cm^4Jyc=∑Jyi+∑Aixci2=4,25+10,2857=14,5357 cm4Jy_c = \sum Jy_i + \sum A_i x_{ci}^2 = 4{,}25 + 10{,}2857 = 14{,}5357\ cm^4Dxyc=∑Dxyi+∑Aixciyci=−1,125−2,5714=−3,6964 cm4Dxy_c = \sum Dxy_i + \sum A_i x_{ci} y_{ci} = -1{,}125 - 2{,}5714 = -3{,}6964\ cm^4

To są centralne momenty bezwładności układu figur.

7. Kąt alfa głównych centralnych osi bezwładności

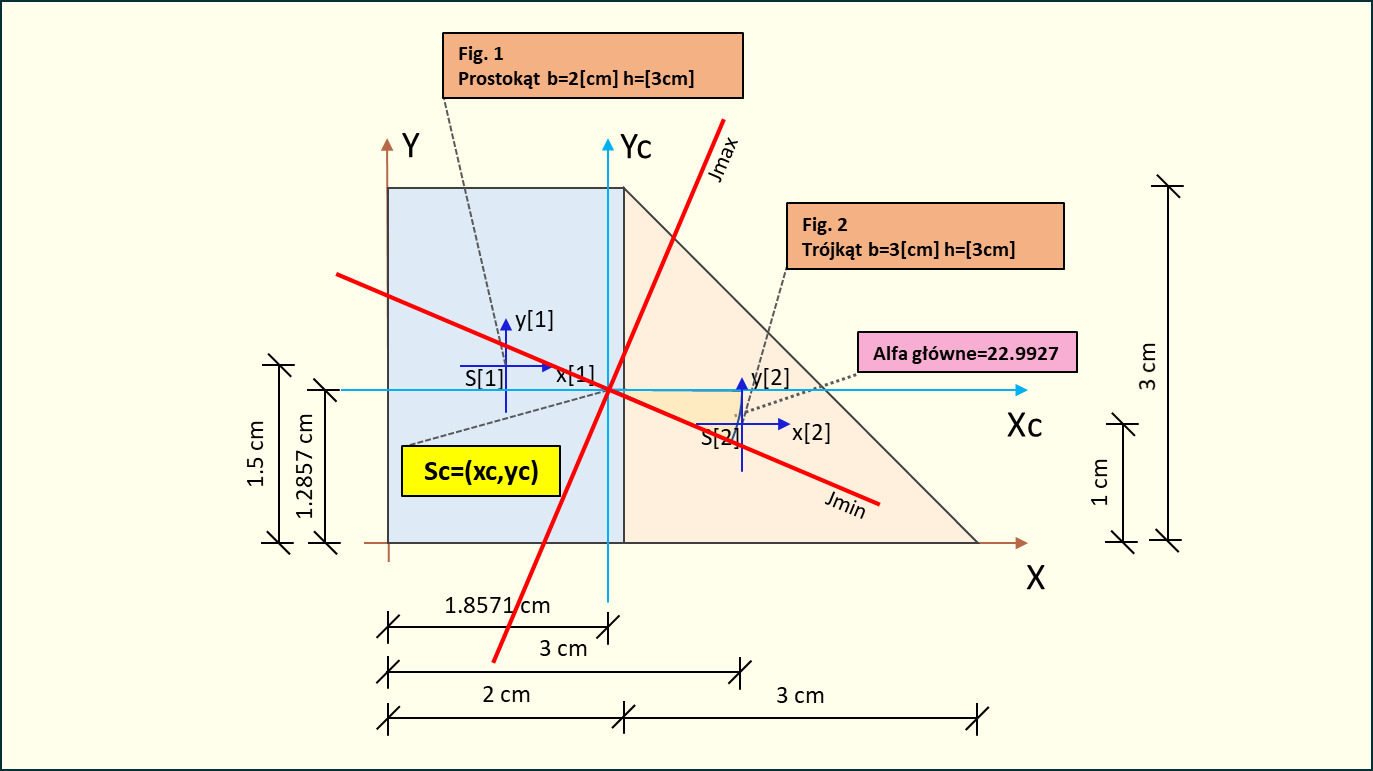
tan⁡2αgl=2DxycJyc−Jxc=2⋅(−3,6964)14,5357−7,3929=−7,39297,1429=−1,0350\tan 2\alpha_{gl} = \frac{2Dxy_c}{Jy_c - Jx_c} = \frac{2 \cdot (-3{,}6964)}{14{,}5357 - 7{,}3929} = \frac{-7{,}3929}{7{,}1429} = -1{,}03502αgl=arctan⁡(tan⁡2αgl)=arctan⁡(−1,035)=−45,9853°2\alpha_{gl} = \arctan(\tan 2\alpha_{gl}) = \arctan(-1{,}035) = -45{,}9853°αgl=22,9927°\alpha_{gl} = 22{,}9927°

Rys. 6. Kąt alfa głównych centralnych osi bezwładności

8. Główne centralne momenty bezwładności

8.1 Jmax
Jmax=Jyc+Jxc2+(Jyc−Jxc2)2+Dxyc2=J_{max} = \frac{Jy_c + Jx_c}{2} + \sqrt{\left(\frac{Jy_c - Jx_c}{2}\right)^2 + Dxy_c^2} ==14,5357+7,39292+(14,5357−7,39292)2+(−3,6964)2== \frac{14{,}5357 + 7{,}3929}{2} + \sqrt{\left(\frac{14{,}5357 - 7{,}3929}{2}\right)^2 + (-3{,}6964)^2} ==10,9643+12,7551+13,6636== 10{,}9643 + \sqrt{12{,}7551 + 13{,}6636} ==10,9643+5,1399== 10{,}9643 + 5{,}1399 =Jmax=16,1042 cm4    (JI)J_{max} = 16{,}1042\ cm^4\ \ \ \ (J_I)
8.2 Jmin
Jmin=Jyc+Jxc2−(Jyc−Jxc2)2+Dxyc2=J_{min} = \frac{Jy_c + Jx_c}{2} - \sqrt{\left(\frac{Jy_c - Jx_c}{2}\right)^2 + Dxy_c^2} ==14,5357+7,39292−(14,5357−7,39292)2+(−3,6964)2== \frac{14{,}5357 + 7{,}3929}{2} - \sqrt{\left(\frac{14{,}5357 - 7{,}3929}{2}\right)^2 + (-3{,}6964)^2} ==10,9643−12,7551+13,6636== 10{,}9643 - \sqrt{12{,}7551 + 13{,}6636} ==10,9643−5,1399== 10{,}9643 - 5{,}1399 =Jmin=5,8244 cm4    (JII)J_{min} = 5{,}8244\ cm^4\ \ \ \ (J_{II})

9. Sprawdzenie

9.1 Niezmiennik J1
δJ1=(Jyc+Jxc)−(Jmax+Jmin)=0\delta J_1 = (Jy_c + Jx_c) - (J_{max} + J_{min}) = 0(Jyc+Jxc)=14,5357+7,3929=21,9286(Jy_c + Jx_c) = 14{,}5357 + 7{,}3929 = 21{,}9286(Jmax+Jmin)=5,8244+16,1042=21,9286(J_{max} + J_{min}) = 5{,}8244 + 16{,}1042 = 21{,}9286δJ1=21,9286−21,9286=0\delta J_1 = 21{,}9286 - 21{,}9286 = 0
9.2 Niezmiennik J2
δJ2=(Jyc⋅Jxc−Dxyc2)−(Jmax⋅Jmin)=0\delta J_2 = (Jy_c \cdot Jx_c - Dxy_c^2) - (J_{max} \cdot J_{min}) = 0(Jyc⋅Jxc−Dxyc2)=14,5357⋅7,3929−13,6636=93,7969(Jy_c \cdot Jx_c - Dxy_c^2) = 14{,}5357 \cdot 7{,}3929 - 13{,}6636 = 93{,}7969(Jmax⋅Jmin)=16,1042⋅5,8244=93,7969(J_{max} \cdot J_{min}) = 16{,}1042 \cdot 5{,}8244 = 93{,}7969δJ2=93,7969−93,7969=0\delta J_2 = 93{,}7969 - 93{,}7969 = 0

10. Momenty bezwładności dla układu XY w punkcie [0,0]

Jx[0,0]=Jxc+∑Ai⋅yc2=7,3929+17,3571=24,75 cm4Jx_{[0,0]} = Jx_c + \sum A_i \cdot y_c^2 = 7{,}3929 + 17{,}3571 = 24{,}75\ cm^4Jy[0,0]=Jyc+∑Ai⋅xc2=14,5357+36,2143=50,75 cm4Jy_{[0,0]} = Jy_c + \sum A_i \cdot x_c^2 = 14{,}5357 + 36{,}2143 = 50{,}75\ cm^4Dxy[0,0]=Dxyc+∑Ai⋅xc⋅yc=−3,6964+10,5⋅1,8571⋅1,2857Dxy_{[0,0]} = Dxy_c + \sum A_i \cdot x_c \cdot y_c = -3{,}6964 + 10{,}5 \cdot 1{,}8571 \cdot 1{,}2857Dxy[0,0]=−3,6964−25,0714=−28,7679 cm4Dxy_{[0,0]} = -3{,}6964 - 25{,}0714 = -28{,}7679\ cm^4

Podsumowanie

W przedstawionym przykładzie wykonaliśmy kompletne obliczenia charakterystyk geometrycznych układu składającego się z prostokąta i trójkąta. Wyznaczyliśmy położenie środka ciężkości układu w punkcie (xc;yc)=(1,8571;1,2857)(x_c; y_c) = (1{,}8571; 1{,}2857) cm, centralne momenty bezwładności (Jxc=7,3929Jx_c = 7{,}3929 cm⁴, Jyc=14,5357Jy_c = 14{,}5357 cm⁴, Dxyc=−3,6964Dxy_c = -3{,}6964 cm⁴), kąt obrotu głównych osi bezwładności (α=22,9927°\alpha = 22{,}9927°) oraz główne centralne momenty bezwładności (Jmax=16,1042J_{max} = 16{,}1042 cm⁴, Jmin=5,8244J_{min} = 5{,}8244 cm⁴). Poprawność obliczeń została potwierdzona przez sprawdzenie niezmienników J1J_1 i J2J_2, które w obu przypadkach wyniosły zero, co świadczy o prawidłowym wykonaniu wszystkich kroków obliczeniowych.

Ostatnia aktualizacja:
Twierdzenie SteineraMomenty bezwładności - przykład nr 2