Momenty bezwładności figur płaskich
Definicja
Momentem bezwładności figury płaskiej nazywamy iloczyn jej pola oraz kwadratu odległości od osi, względem której jest on liczony.
Moment bezwładności zazwyczaj jest wyrażany w jednostkach długości do czwartej potęgi (, , itd.). Im większy moment bezwładności względem danej osi, tym przekrój jest sztywniejszy, a co za tym idzie, ugięcie powstałe w wyniku przyłożenia siły będzie mniejsze.
Przykład praktyczny
Rozważmy praktyczne zastosowanie momentów bezwładności w projektowaniu konstrukcji.
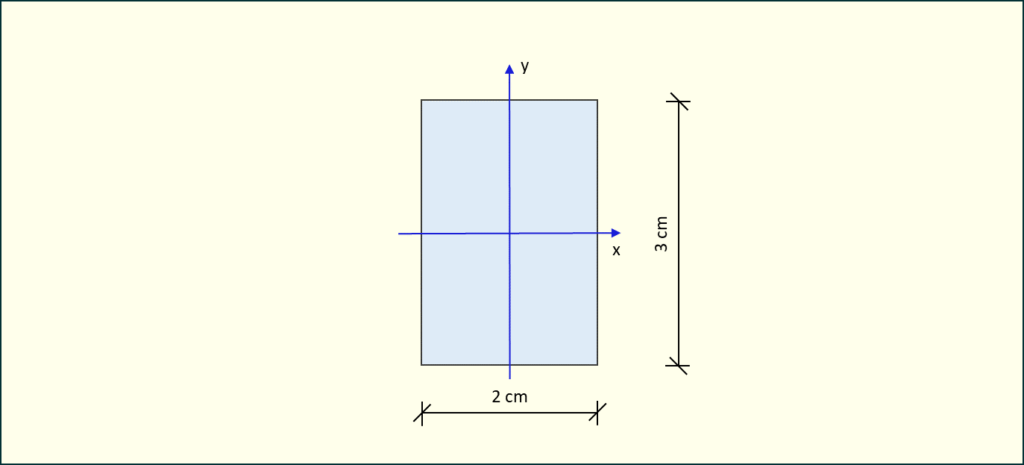
Rys. 1. Przekrój poprzeczny belki
Wyobraźmy sobie, że powyższy rysunek przedstawia przekrój poprzeczny belki. Naszym zadaniem jest sprawdzić w jakiej pozycji ją ustawić, aby ugięcie po obciążeniu było najmniejsze. Musimy zatem obliczyć momenty bezwładności tego przekroju względem każdej z osi znajdujących się w centrum figury.
Dla przedstawionego przekroju prostokątnego o wymiarach i momenty bezwładności obliczamy następująco:
Wzory na momenty bezwładności figur płaskich możemy znaleźć w tablicach inżynierskich. W przypadku kształtowników tablice często sporządza sam producent.
Porównując obliczone wartości widzimy, że:
Wynika z tego, że belkę najlepiej ustawić w pozycji, w której jej oś x będzie prostopadła do kierunku przyłożonej siły. Dokładnie jak na rysunku poniżej.
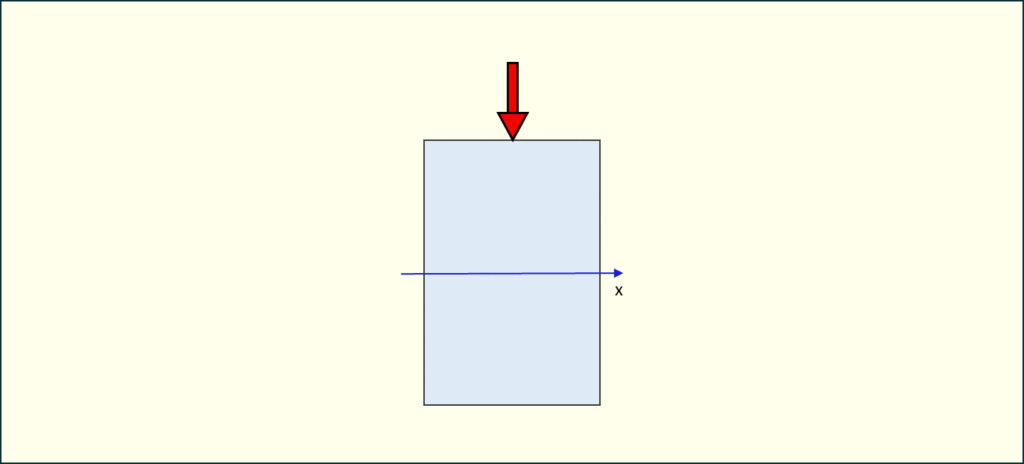
Rys. 5. Optymalna orientacja belki
Wzory i tablice
W tabeli poniżej przedstawiono parametry geometryczne najczęściej spotykanych figur płaskich.
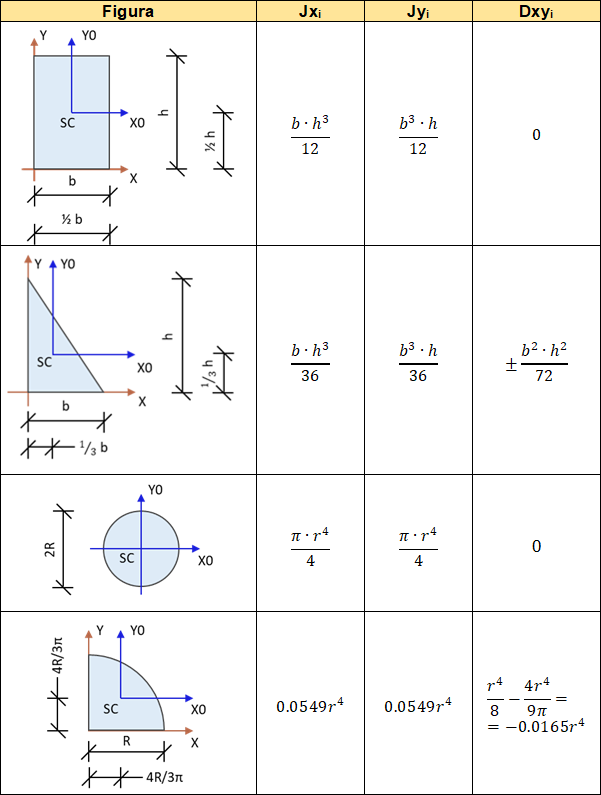
Rys. 2. Tablica wzorów na momenty bezwładności podstawowych figur