Moment zginający
Moment zginający nazywamy parę sił, które powodują obrót elementu. Wzór określający wartość momentu działającego w danym punkcie:
Gdzie:
- – moment zginający
- – siła działająca na dany element
- – ramię siły, czyli odległość siły do punktu, względem którego liczymy moment
Znak momentu zginającego
Znak wartości momentu zależy od kierunku działania momentu na dany punkt. Zazwyczaj przyjmuje się, że:
- Moment zgodny ze wskazówkami zegara → znak dodatni (+)
- Moment przeciwny do wskazówek zegara → znak ujemny (-)
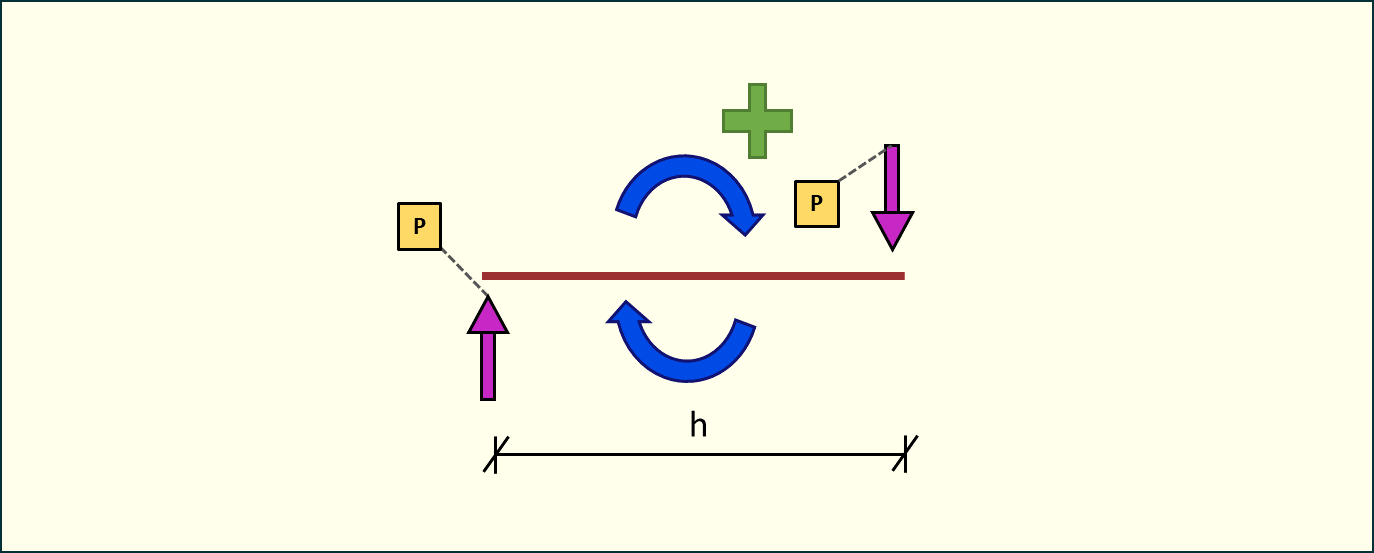
Rys. 1. Moment dodatni - obrót w prawo
Jak widać na powyższym rysunku para sił na ramieniu powoduje obrót elementu w prawo, czyli moment będzie miał znak dodatni.
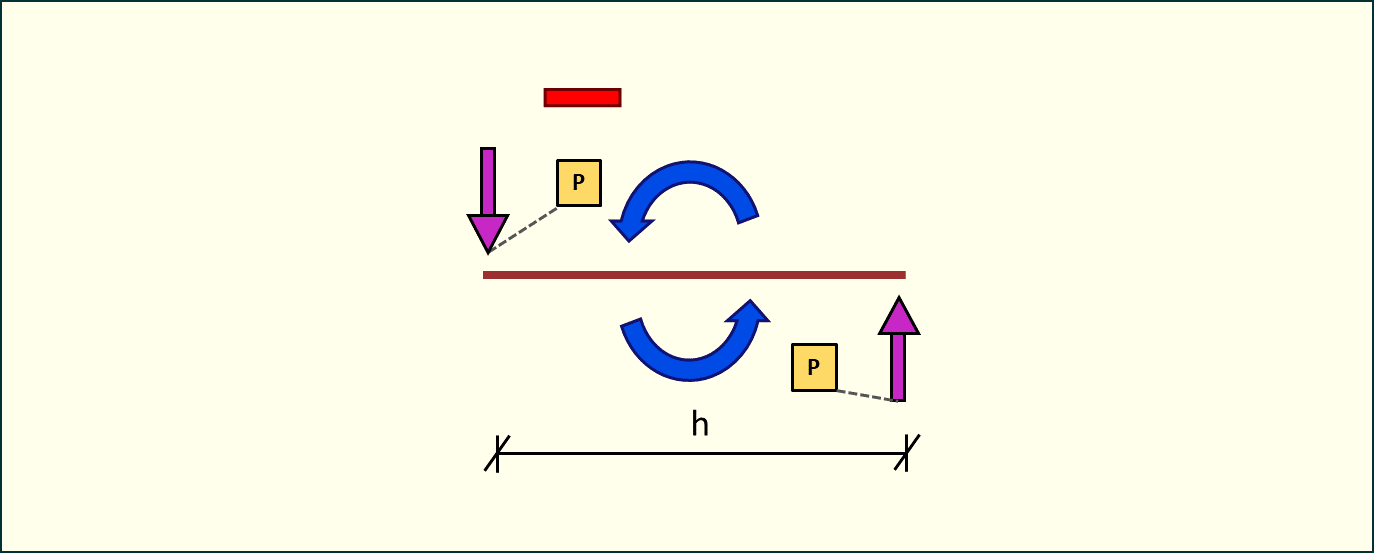
Rys. 2. Moment ujemny - obrót w lewo
Patrząc na rysunek powyżej widzimy sytuację odwrotną i wartość momentu będzie ujemna.
Uwaga: Jeżeli siła przechodzi przez punkt, względem którego liczymy wartość momentu, to nie powoduje ona obrotu elementu i wartość momentu od tej siły wynosi zero (, więc ).
Przykład obliczenia sumy momentów
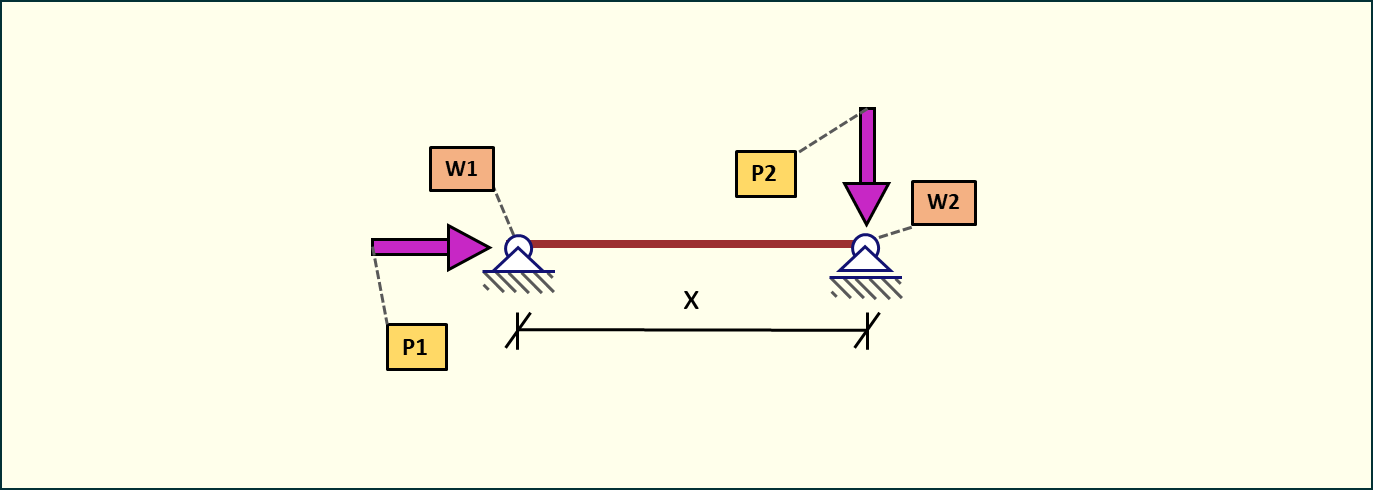
Rys. 3. Belka z dwiema siłami P1 i P2
Mamy belkę, na którą działają dwie siły i .
Suma momentów względem punktu podparcia na podporze W1:
Siła działa na ramieniu zerowym, bo przechodzi przez punkt . Siła działa na ramieniu , ponieważ znajduje się w odległości od punktu podparcia belki na podporze .
Suma momentów względem punktu podparcia na podporze W2:
Wynika to z faktu, że obie siły przechodzą przez punkt podparcia belki na podporze , zatem wartość ramion, na których działają obie siły, wynosi zero.
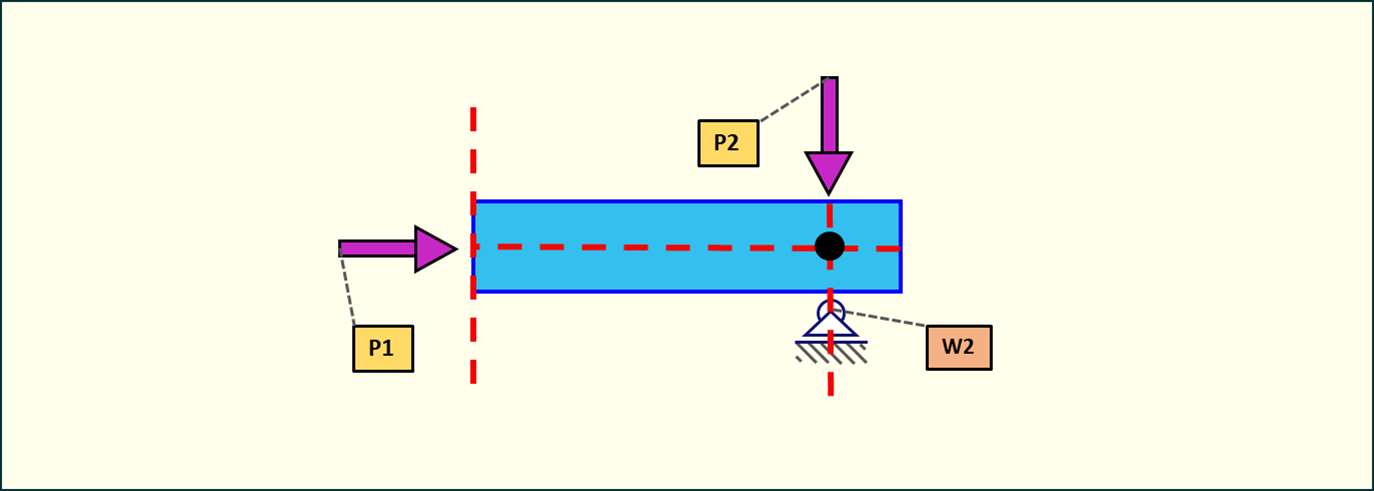
Rys. 4. Siły działające w osi belki
Zakładamy, że obie siły działają w osiach belki, czyli jak przedstawiono na rysunku powyżej. Mimo że do obliczeń zakładamy, że belka jest elementem bardzo cienkim, w rzeczywistości ma ona przekrój o odpowiednich wymiarach. Punkt podparcia na podporze to czarna kropka.
Zazwyczaj rozpatrując dany element konstrukcyjny zakładamy, że siły działają w osiach przekroju elementu. Pozwala nam to uprościć rysunek belki i sprowadzić go do linii prostej.