Kącik Wiedzy
Metoda Równoważenia Węzłów

Metoda Równoważenia Węzłów

maja 22, 2018

Wprowadzenie

Metoda równoważenia węzłów to podstawowa metoda analityczna służąca do obliczania sił wewnętrznych w prętach kratownic statycznie wyznaczalnych. Metoda ta polega na analizie równowagi sił w każdym węźle konstrukcji, sprawdzając czy sumy rzutów wszystkich sił na oś x oraz y w danym węźle będą wynosić zero.

Przykład obliczeniowy

Rozpatrzmy kratownicę przedstawioną poniżej. Celem jest obliczenie sił w poszczególnych prętach.

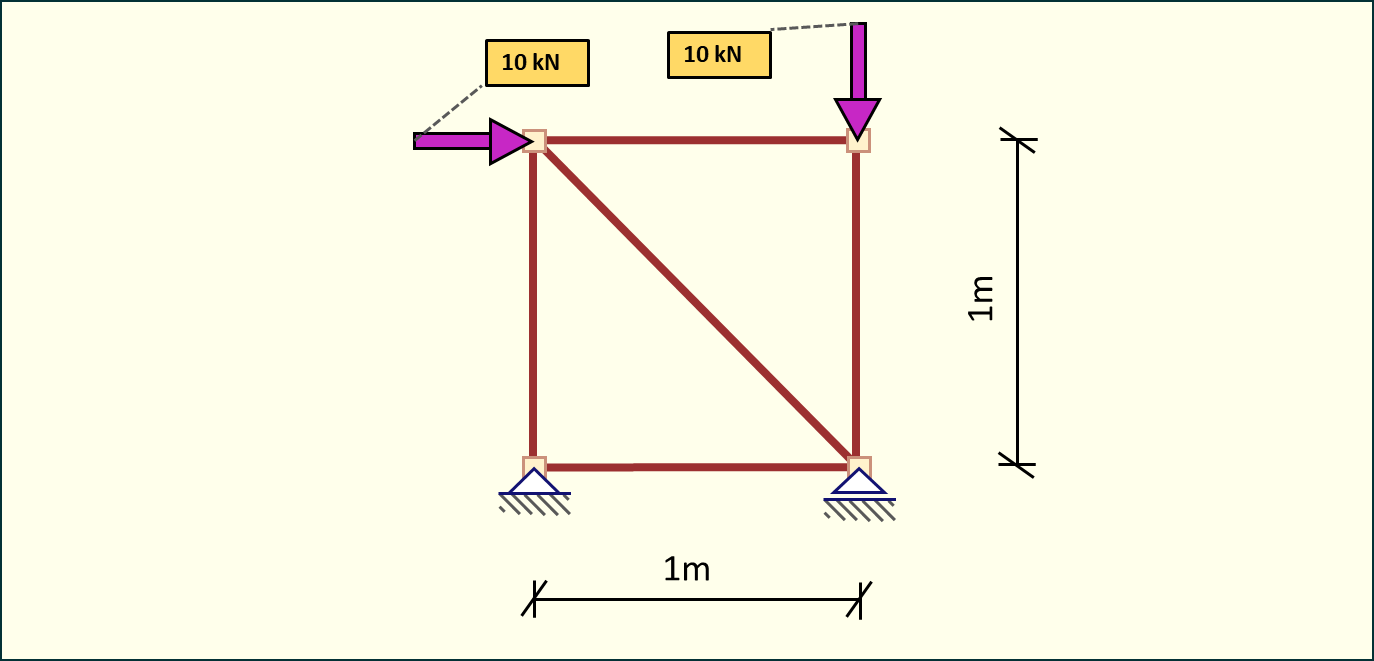
Rys. 1. Schemat statyczny kratownicy

1. Reakcje podporowe

Pierwszym etapem analizy jest wyznaczenie reakcji podporowych.

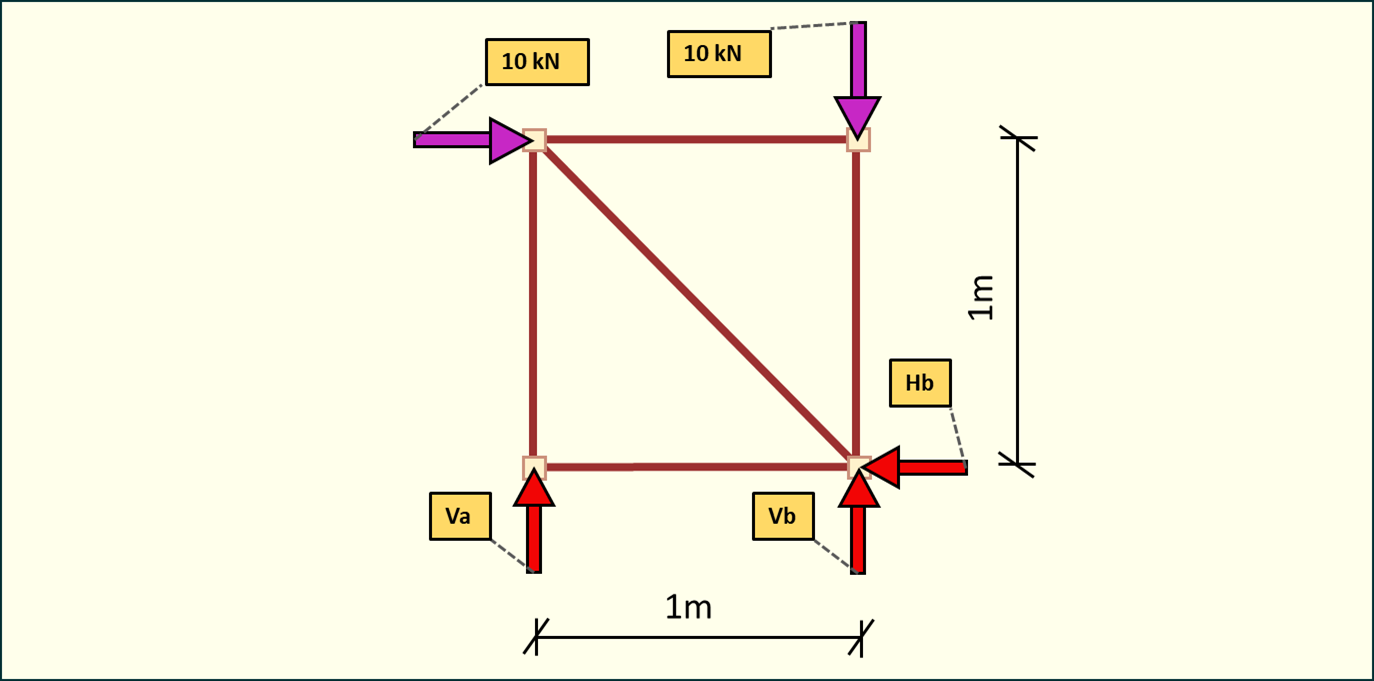
Rys. 2. Schemat do obliczenia reakcji podporowych

Policzmy najpierw sumę momentów względem punktu podparcia na podporze B.

∑MB=0\sum M_B = 0

VA⋅1m+10 kN⋅1m=0V_A \cdot 1m + 10\ kN \cdot 1m = 0

VA=−10 kNV_A = -10\ kN

Znając wartość reakcji na podporze A możemy obliczyć VBV_B korzystając z sumy rzutów na oś x.

∑Px=0\sum P_x = 0

−VA−VB+10 kN=0-V_A - V_B + 10\ kN = 0

−(−10kN)−VB+10 kN=0-(-10kN) - V_B + 10\ kN = 0

VB=0V_B = 0

Następnie możemy skorzystać z sumy rzutów na oś y.

∑Py=0\sum P_y = 0

10 kN−HB=010\ kN - H_B = 0

HB=10 kNH_B = 10\ kN

2. Analiza węzłów kratownicy

Znając wszystkie reakcje podporowe, możemy przejść do obliczania sił w prętach kratownicy, analizując równowagę poszczególnych węzłów.

2.1. Węzeł podporowy A

Jako pierwszy rozpatrzymy węzeł podporowy A.

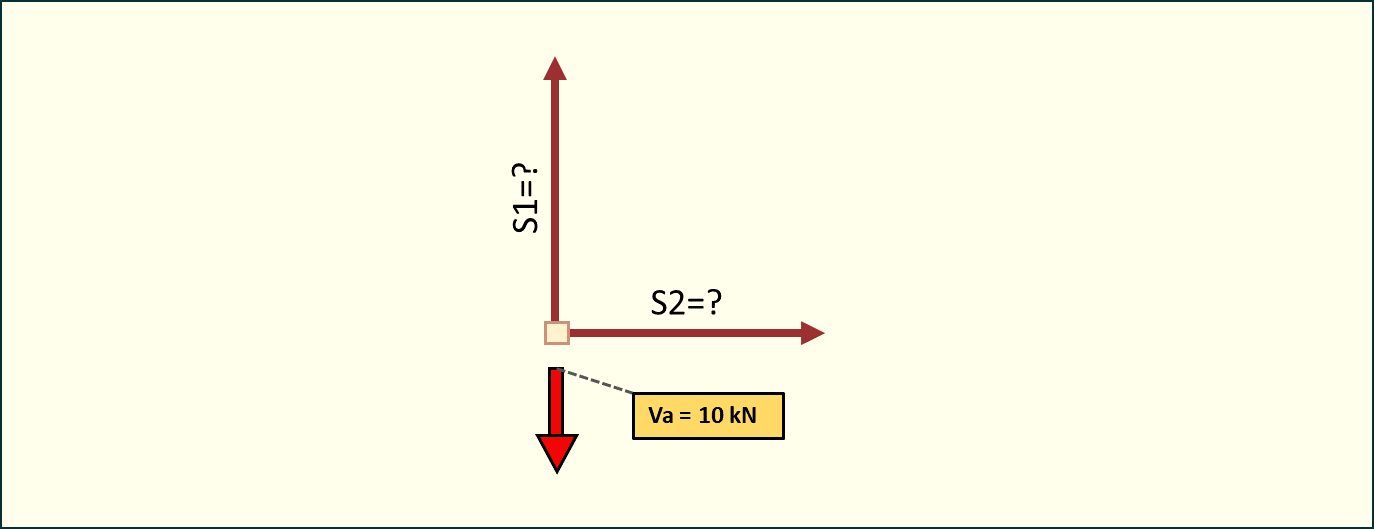
Rys. 6. Analiza węzła A

∑Px=0\sum P_x = 0

VA−S1=0V_A - S_1 = 0

VA=S1V_A = S_1

S1=10 kNS_1 = 10\ kN
∑Py=0\sum P_y = 0

S2=0S_2 = 0
2.2. Węzeł podporowy B

Poznaliśmy wartości sił w dwóch pierwszych prętach. Teraz pora na węzeł podporowy B.

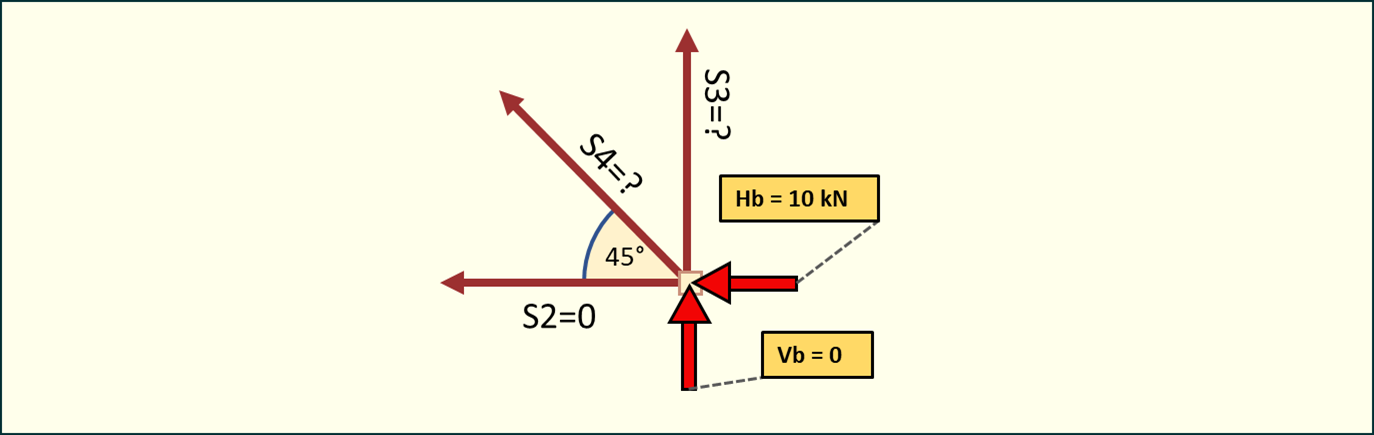
Rys. 9. Analiza węzła B

∑Px=0\sum P_x = 0

−S3−VB=0-S_3 - V_B = 0

S3=0S_3 = 0
∑Py=0\sum P_y = 0

−S2−HB−S4⋅cos⁡(45°)=0-S_2 - H_B - S_4 \cdot \cos(45°) = 0

−0−10kN−S4⋅0.71=0-0 - 10kN - S_4 \cdot 0.71 = 0

S4⋅0.71=−10kNS_4 \cdot 0.71 = -10kN

S4=−14,08kNS_4 = -14{,}08kN
2.3. Ostatni węzeł - pręt górny

Została nam jeszcze do policzenia siła w pręcie górnym.

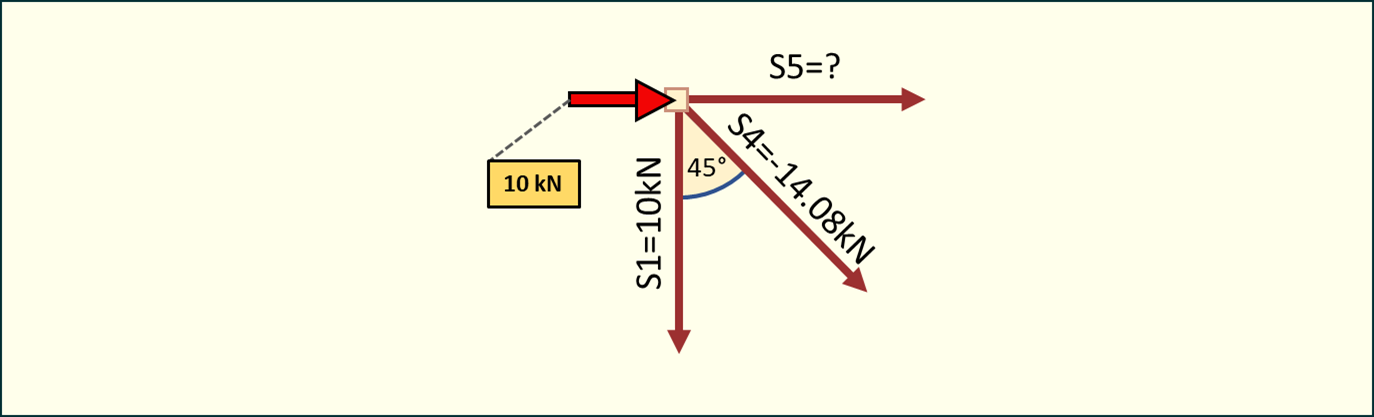
Rys. 12. Analiza ostatniego węzła - pręt górny

∑Py=0\sum P_y = 0

10 kN+S4⋅cos⁡(45°)+S5=010\ kN + S_4 \cdot \cos(45°) + S_5 = 0

10kN−14,08⋅0,71+S5=010kN - 14{,}08 \cdot 0{,}71 + S_5 = 0

S5=0S_5 = 0

Podsumowanie

Metoda równoważenia węzłów pozwala systematycznie obliczyć siły we wszystkich prętach kratownicy poprzez analizę równowagi każdego węzła z osobna. Kluczowe jest przestrzeganie kolejności analizy węzłów - zaczynamy od węzłów, w których mamy co najwyżej dwie niewiadome siły. Po wyznaczeniu sił w jednym węźle, przesuwamy się do kolejnego, gdzie znane już siły z poprzednich obliczeń redukują liczbę niewiadomych.

Ostatnia aktualizacja:
Identyfikacja prętów zerowych kratownicyObliczanie sił w węzłach kratownic metodą Rittera