Obliczanie sił w węzłach kratownic metodą Rittera
Wprowadzenie
Metoda Rittera (metoda przekrojów) to alternatywny sposób obliczania sił w prętach kratownic statycznie wyznaczalnych. Jest szczególnie przydatna gdy chcemy obliczyć siłę w wybranym pręcie bez konieczności analizowania wszystkich węzłów. Metoda ta często jest używana do:
- Sprawdzenia wyników uzyskanych metodą równoważenia węzłów
- Szybkiego obliczenia sił w konkretnych prętach
W wielu przypadkach metoda Rittera jest znacznie szybsza niż metoda równoważenia węzłów.
Zasada działania metody
Metoda Rittera polega na przecięciu kratownicy płaszczyzną przechodzącą przez maksymalnie trzy pręty, których siły chcemy obliczyć. Następnie rozpatrujemy równowagę jednej z części przeciętej kratownicy, wybierając odpowiednie punkty do obliczania momentów tak, aby w każdym równaniu była tylko jedna niewiadoma.
Kluczowe zasady:
Przecięcie powinno przechodzić przez nie więcej niż trzy pręty (w kratownicach statycznie wyznaczalnych)
Punkty, względem których obliczana jest suma momentów, dobiera się tak, aby leżały na liniach działania dwóch z przeciętych prętów
Dzięki temu w równaniu momentów pozostaje tylko jedna niewiadoma siła
Przykład obliczeniowy
Rozpatrzmy tę samą kratownicę co w poprzednim przykładzie (metoda równoważenia węzłów) i obliczmy siły w prętach metodą Rittera. Reakcje podporowe zostały już obliczone: , i .
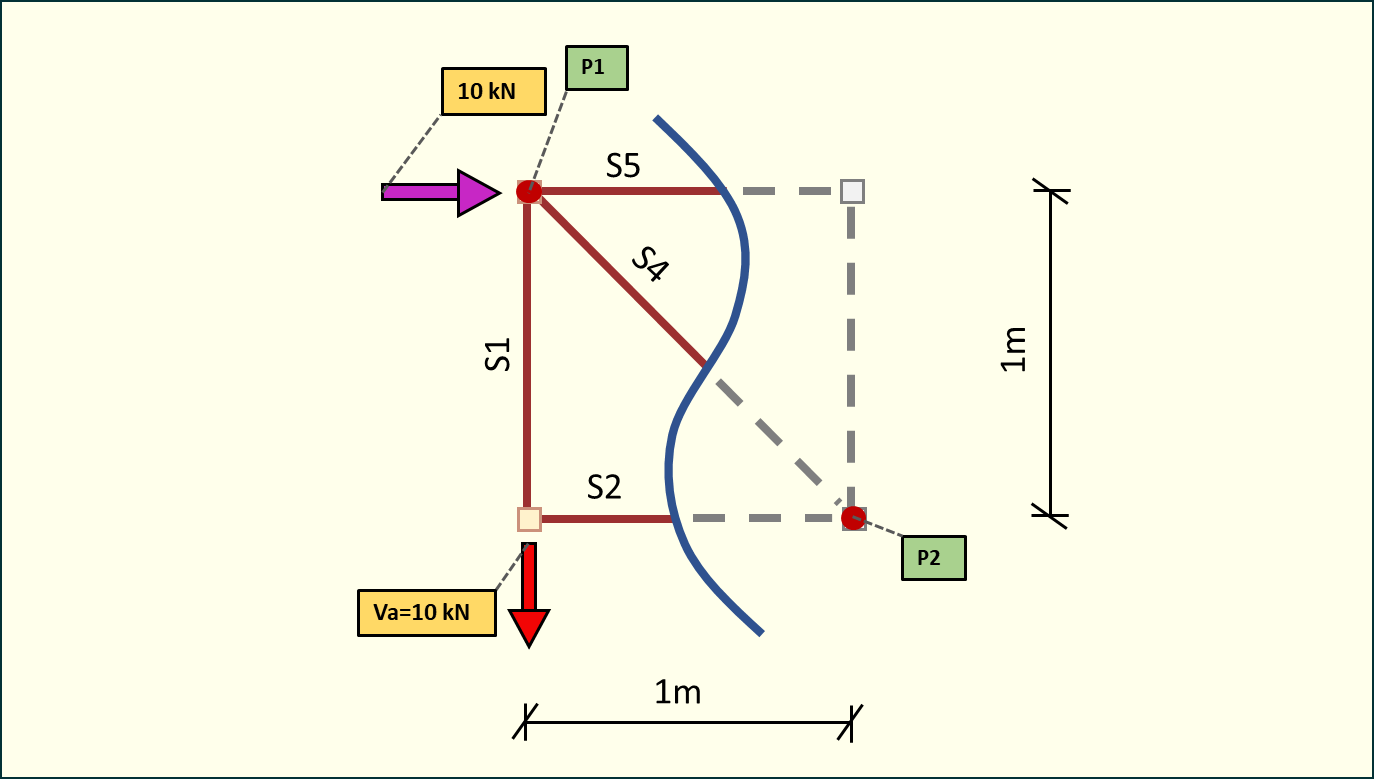
Rys. 3. Przecięcie kratownicy - metoda Rittera
Na powyższym rysunku mamy przykład cięcia metodą Rittera przez 3 pręty kratownicy (, , ). Spróbujmy obliczyć siły w tych prętach wykorzystując sumę momentów względem punktów P1 i P2.
Obliczenie siły w pręcie S2
Wybieramy punkt P1, przez który przechodzą pręty i . Dzięki temu ramię działania tych sił wynosi zero, a w równaniu pozostaje tylko siła .
Obliczenie siły w pręcie S5
Wybieramy punkt P2, przez który przechodzą pręty i . W równaniu pozostaje tylko siła .
W tym konkretnym przypadku większość sił w prętach jest zerowa (co zgadza się z wynikami metody równoważenia węzłów - i to pręty zerowe), ale sama procedura obliczeniowa pozostaje taka sama niezależnie od wartości wyników.
Podsumowanie
Metoda Rittera jest potężnym narzędziem do analizy kratownic. Jej główne zalety to:
- Szybkość - możliwość obliczenia siły w wybranym pręcie bez analizowania wszystkich węzłów
- Weryfikacja - doskonale nadaje się do sprawdzenia wyników uzyskanych inną metodą
Kluczową umiejętnością przy stosowaniu metody Rittera jest odpowiedni dobór punktów, względem których obliczamy sumę momentów. Punkt powinien leżeć na przecięciu linii działania dwóch prętów, których sił nie chcemy uwzględniać w danym równaniu.