Kącik Wiedzy
Metoda Przemieszczeń

Metoda Przemieszczeń

maja 7, 2019

Wprowadzenie

Metoda przemieszczeń – metoda zwana także metodą odkształceń, pozwalająca obliczać układy statycznie niewyznaczalne.

Co to są układy statycznie niewyznaczalne, możesz dowiedzieć się w artykule Konstrukcje statycznie niewyznaczalne.

Algorytm obliczeń

  1. Wyznaczanie stopnia kinematycznej niewyznaczalności układu
  2. Przyjęcie układu podstawowego i układu równań kanonicznych
  3. Obliczenie łańcucha kinematycznego
  4. Obliczanie układu równań kanonicznych (macierz sztywności)
  5. Obliczanie momentów przywęzłowych, sił tnących i sił normalnych
  6. Obliczenie i sprawdzanie reakcji podporowych

Przykład obliczeniowy

Zadanie: Wyznaczyć wykresy M, T, N dla ramy przedstawionej na poniższym schemacie przy pomocy metody przemieszczeń.

1. Schemat zadania

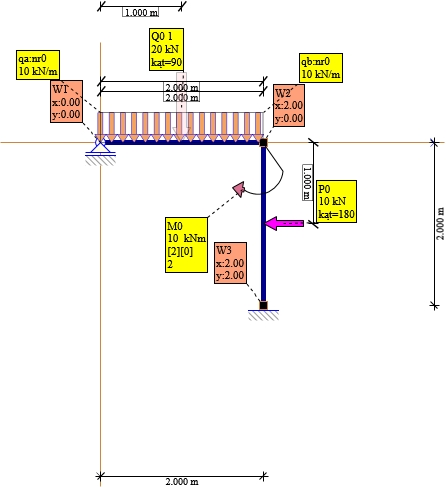
Rys. 1. Schemat układu

Współrzędne węzłów:

  • Węzeł 1: x = 0.000 m, y = 0.000 m
  • Węzeł 2: x = 2.000 m, y = 0.000 m
  • Węzeł 3: x = 2.000 m, y = 2.000 m

Przyjęto przekrój podstawowy:

  • I = 3060 cm⁴
  • E = 205 GPa
  • Globalne EI = 6273 kNm²
  • Globalne EA = 809750 kN

2. Ustalenie stopnia kinematycznej niewyznaczalności układu (SKN)

Węzły o nieznanych obrotach:

φ = 1 = węzły - podpory - przeguby

SKN = φ + Δ = 2

Układ jest 2-krotnie kinematycznie niewyznaczalny.

3. Przyjęcie układu podstawowego

Układ równań kanonicznych:

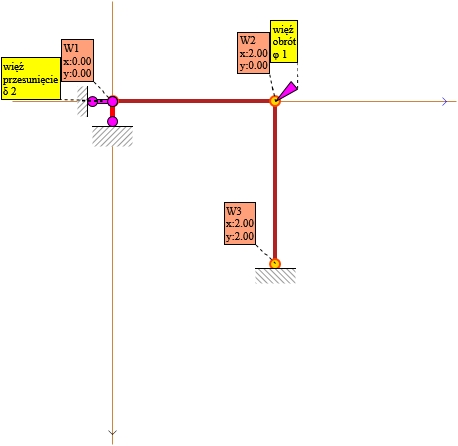
[r1−1r1−2r2−1r2−2][φ1δ2]+[r1Pr2P]=[00]\begin{bmatrix} r_{1-1} & r_{1-2} \\ r_{2-1} & r_{2-2} \end{bmatrix} \begin{bmatrix} \varphi_1 \\ \delta_2 \end{bmatrix} + \begin{bmatrix} r_{1P} \\ r_{2P} \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix}

Rys. 2. Układ podstawowy metody przemieszczeń

4. Obliczenie zależności kątowych obrotu cięciw prętów układu

Obliczenie zależności kątowych obrotu cięciw prętów układu potrzebnych do wyznaczenia macierzy sztywności dla stanu Stan δ₂, Δ=1.

Wybieram węzeł przesuwany 1.

Węzeł przemieści się wtedy o:

dx=Δ⋅sin⁡β=1⋅(−1)=1dx = \Delta \cdot \sin\beta = 1 \cdot (-1) = 1dy=−Δ⋅cos⁡β=1⋅0=0dy = -\Delta \cdot \cos\beta = 1 \cdot 0 = 0

Przyjęte przemieszczenie i kąt podstawiam do łańcuchów kinematycznych jako wiadome.

Łańcuch obliczany: 1-2, 2-3

{↓Ψ1−2(2−0)+Ψ2−3(2−2)=(0)→Ψ1−2(0−0)+Ψ2−3(0−2)=(−1)\begin{cases} \downarrow \quad \Psi_{1-2}(2-0) + \Psi_{2-3}(2-2) = (0) \\ \rightarrow \quad \Psi_{1-2}(0-0) + \Psi_{2-3}(0-2) = (-1) \end{cases}{↓Ψ1−2⋅2+Ψ2−3⋅0=(0)→Ψ1−2⋅0+Ψ2−3⋅(−2)=(−1)\begin{cases} \downarrow \quad \Psi_{1-2} \cdot 2 + \Psi_{2-3} \cdot 0 = (0) \\ \rightarrow \quad \Psi_{1-2} \cdot 0 + \Psi_{2-3} \cdot (-2) = (-1) \end{cases}{↓Ψ1−2⋅2+Ψ2−3⋅0=(0)→Ψ1−2⋅0+Ψ2−3⋅(−2)=(−1)\begin{cases} \downarrow \quad \Psi_{1-2} \cdot 2 + \Psi_{2-3} \cdot 0 = (0) \\ \rightarrow \quad \Psi_{1-2} \cdot 0 + \Psi_{2-3} \cdot (-2) = (-1) \end{cases}

Po obliczeniu równania:

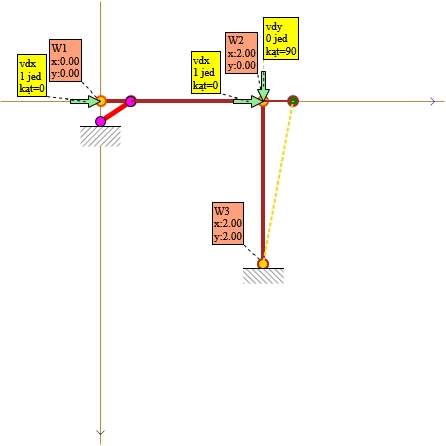
Ψ1−2=(0)1m\Psi_{1-2} = (0)\frac{1}{m}Ψ2−3=0.51m\Psi_{2-3} = 0.5\frac{1}{m}

Rys. 3. Łańcuch kinematyczny Stan δ2 Δ=1

5. Stan φ₁

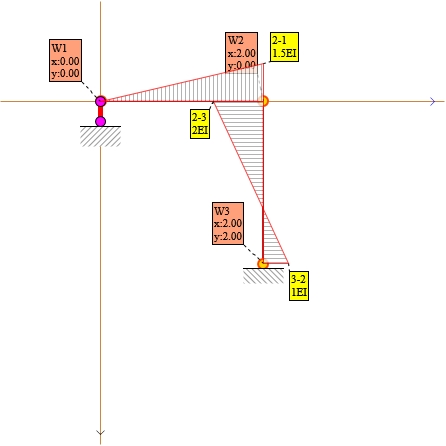
M2−1=3⋅EIL=3⋅12=1.5EImM_{2-1} = \frac{3 \cdot EI}{L} = \frac{3 \cdot 1}{2} = 1.5\frac{EI}{m}M2−3=4⋅EIL=4⋅12=2EImM_{2-3} = \frac{4 \cdot EI}{L} = \frac{4 \cdot 1}{2} = 2\frac{EI}{m}M1−2=0EImM_{1-2} = 0\frac{EI}{m}M3−2=2⋅EIL=2⋅12=1EImM_{3-2} = \frac{2 \cdot EI}{L} = \frac{2 \cdot 1}{2} = 1\frac{EI}{m}

Rys. 4. Stan φ₁

6. Stan δ₂

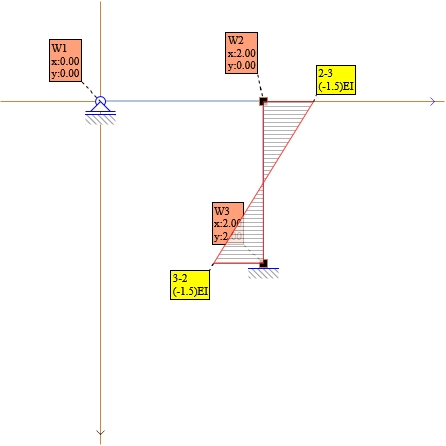
M2−3=−Δ2−3⋅6⋅EIL2=−1⋅6⋅I4=(−1.5)EIm2M_{2-3} = -\frac{\Delta_{2-3} \cdot 6 \cdot EI}{L^2} = -\frac{1 \cdot 6 \cdot I}{4} = (-1.5)\frac{EI}{m^2}M3−2=−Δ2−3⋅6⋅EIL2=−1⋅6⋅I4=(−1.5)EIm2M_{3-2} = -\frac{\Delta_{2-3} \cdot 6 \cdot EI}{L^2} = -\frac{1 \cdot 6 \cdot I}{4} = (-1.5)\frac{EI}{m^2}

Rys. 5. Stan δ₂

7. Stan P - obciążenie mpq

q pręt = 1-2:

M1−2=0 kNmM_{1-2} = 0\ \text{kNm}M2−1=10⋅2⋅18⋅22[4(22−12)−22]=5 kNmM_{2-1} = \frac{10 \cdot 2 \cdot 1}{8 \cdot 2^2} \left[4(2^2 - 1^2) - 2^2\right] = 5\ \text{kNm}

P pręt = 2-3:

M2−3=−10⋅1⋅1222=(−2.5) kNmM_{2-3} = -\frac{10 \cdot 1 \cdot 1^2}{2^2} = (-2.5)\ \text{kNm}M3−2=10⋅1⋅1222=2.5 kNmM_{3-2} = \frac{10 \cdot 1 \cdot 1^2}{2^2} = 2.5\ \text{kNm}

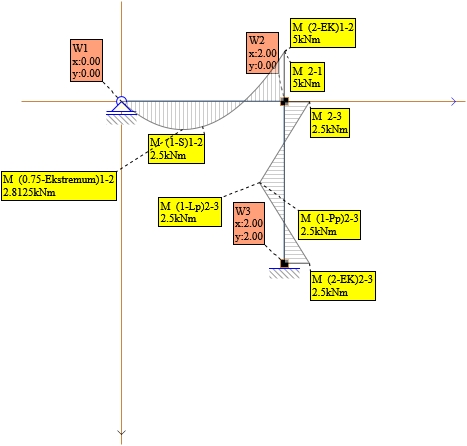
Rys. 6. Stan P

8. Współczynniki macierzy sztywności i wyrazów wolnych

r1−1=∑jM1j1+k1φr_{1-1} = \sum_j M_{1j}^1 + k_1^\varphir1−1=1.5EIm+2EIm=3.5EImr_{1-1} = 1.5\frac{EI}{m} + 2\frac{EI}{m} = 3.5\frac{EI}{m}r1−2=∑jM1−j2r_{1-2} = \sum_j M_{1-j}^2r1−2=(−1.5)EIm2+(−1.5)EIm2r_{1-2} = (-1.5)\frac{EI}{m^2} + (-1.5)\frac{EI}{m^2}r2−2=−∑ij(Mij2+Mji2)Ψij2+∑jkjδδj2δj2r_{2-2} = -\sum_{ij}\left(M_{ij}^2 + M_{ji}^2\right)\Psi_{ij}^2 + \sum_j k_j^\delta \delta_j^2 \delta_j^2r2−2=−((−1.5)+(−1.5))⋅0.5EIm2=1.5EIm2r_{2-2} = -((-1.5) + (-1.5)) \cdot 0.5\frac{EI}{m^2} = 1.5\frac{EI}{m^2}r2−1=−∑ij(Mij1+Mji1)Ψij2r_{2-1} = -\sum_{ij}\left(M_{ij}^1 + M_{ji}^1\right)\Psi_{ij}^2r2−1=−(0+1.5)⋅(0)EIm2−(2+1)⋅0.5EIm2=(−1.5)EIm2r_{2-1} = -(0 + 1.5) \cdot (0)\frac{EI}{m^2} - (2 + 1) \cdot 0.5\frac{EI}{m^2} = (-1.5)\frac{EI}{m^2}r1−P=∑jM1jP−M1Pr_{1-P} = \sum_j M_{1j}^P - M_1^Pr1−P=5+(−2.5)+(−10)=(−7.5) kNmr_{1-P} = 5 + (-2.5) + (-10) = (-7.5)\ \text{kNm}r2−P=−∑ij(MijP+MjiP)Ψij2+∑PPp⋅δp2r_{2-P} = -\sum_{ij}\left(M_{ij}^P + M_{ji}^P\right)\Psi_{ij}^2 + \sum_{P} P_p \cdot \delta_p^2r2−P=((−2.5)+2.5)⋅0.5+0⋅1+20⋅0+(−10)⋅0.5+0+0=5 kNr_{2-P} = ((-2.5) + 2.5) \cdot 0.5 + 0 \cdot 1 + 20 \cdot 0 + (-10) \cdot 0.5 + 0 + 0 = 5\ \text{kN}

9. Układ równań kanonicznych

[3.5(−1.5)(−1.5)1.5][∣φ1∣∣δ2∣]=[(−7.5)5]=[00]\begin{bmatrix} 3.5 & (-1.5) \\ (-1.5) & 1.5 \end{bmatrix} \begin{bmatrix} |\varphi_1| \\ |\delta_2| \end{bmatrix} = \begin{bmatrix} (-7.5) \\ 5 \end{bmatrix} = \begin{bmatrix} 0 \\ 0 \end{bmatrix}

Po rozwiązaniu układu otrzymano:

φ1=1.25⋯kN⋅m2EI\varphi_1 = 1.25 \cdots \frac{kN \cdot m^2}{EI}δ2=(−2.08333)⋯kN⋅m3EI\delta_2 = (-2.08333) \cdots \frac{kN \cdot m^3}{EI}

10. Obliczenie momentów przywęzłowych

Zgodnie ze wzorem:

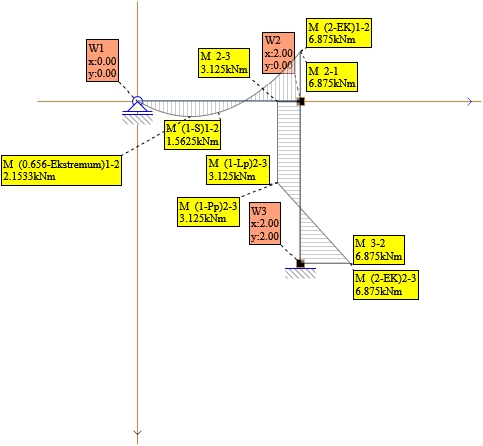
Mik=Mik0+Mik1⋅φ1+Mik2⋅δ2M_{ik} = M_{ik}^0 + M_{ik}^1 \cdot \varphi_1 + M_{ik}^2 \cdot \delta_2Mki=Mki0+Mki1⋅φ1+Mki2⋅δ2M_{ki} = M_{ki}^0 + M_{ki}^1 \cdot \varphi_1 + M_{ki}^2 \cdot \delta_2
M1−2=0⋅1.25+0⋅1=0 kNmM_{1-2} = 0 \cdot 1.25 + 0 \cdot 1 = 0\ \text{kNm}M2−1=1.5⋅1.25+5⋅1=6.875 kNmM_{2-1} = 1.5 \cdot 1.25 + 5 \cdot 1 = 6.875\ \text{kNm}M2−3=2⋅1.25+(−1.5)⋅(−2.08333)+(−2.5)⋅1=3.125 kNmM_{2-3} = 2 \cdot 1.25 + (-1.5) \cdot (-2.08333) + (-2.5) \cdot 1 = 3.125\ \text{kNm}M3−2=1⋅1.25+(−1.5)⋅(−2.08333)+2.5⋅1=6.875 kNmM_{3-2} = 1 \cdot 1.25 + (-1.5) \cdot (-2.08333) + 2.5 \cdot 1 = 6.875\ \text{kNm}

Rys. 7. Wykres M

11. Obliczenie sił tnących

Pręt 1-2:

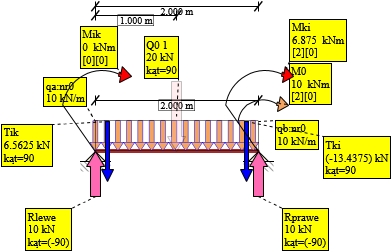
Rys. 8. Siły tnące 1-2

T1−2=0+(−6.875)2−(−10)=6.5625 kNT_{1-2} = \frac{0 + (-6.875)}{2} - (-10) = 6.5625\ \text{kN}T2−1=0+(−6.875)2+(−10)=(−13,4375) kNT_{2-1} = \frac{0 + (-6.875)}{2} + (-10) = (-13{,}4375)\ \text{kN}

Pręt 2-3:

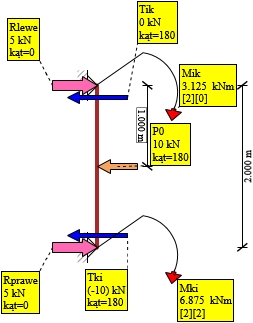
Rys. 9. Siły tnące 2-3

T2−3=(−3.125)+(−6.875)2−(−5)=0 kNT_{2-3} = \frac{(-3.125) + (-6.875)}{2} - (-5) = 0\ \text{kN}T3−2=(−3.125)+(−6.875)2+(−5)=(−10) kNT_{3-2} = \frac{(-3.125) + (-6.875)}{2} + (-5) = (-10)\ \text{kN}

Wykres T:

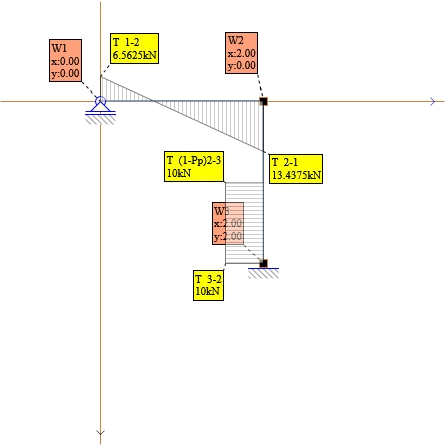
Rys. 10. Wykres T

12. Obliczenie sił normalnych

Aby węzeł był w równowadze, suma jego składowych sił i reakcji rzutowana na oś X i oś Y musi być równa zero:

∑Sx+∑Rx+∑Px=0\sum Sx + \sum Rx + \sum Px = 0∑Sy+∑Ry+∑Py=0\sum Sy + \sum Ry + \sum Py = 0

Gdzie:

  • ΣSx - suma sił prętowych rzutowana na oś X w węźle
  • ΣRx - suma reakcji podporowych rzutowana na oś X w węźle (jeżeli istnieje)
  • ΣPx - suma oddziaływania zewnętrznego rzutowana na oś X w węźle (jeżeli jest przyłożona)
  • ΣSy - suma sił prętowych rzutowana na oś Y w węźle
  • ΣRy - suma reakcji podporowych rzutowana na oś Y w węźle (jeżeli istnieje)
  • ΣPy - suma oddziaływania zewnętrznego rzutowana na oś Y w węźle (jeżeli jest przyłożona)

Obliczenia rozpoczynamy od węzła, dla którego liczba niewiadomych sił w prętach jest ≤ 2.

Elementy szukane oznaczono kolorem czerwonym. Elementy zerowe są przedstawione w tle rysunku.

Wybrano węzeł 1:

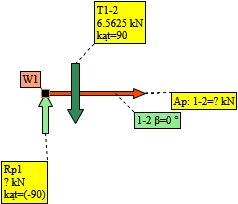
Rys. 11. Analiza węzła 1 - schemat

Do policzenia N1−2β=0\text{Do policzenia } N_{1-2}\quad \beta = 0

Rzutowanie na oś X

N1−2⋅cos⁡(0)=0N_{1-2}\cdot \cos(0) = 0

N1−2⋅cos⁡(0)=0N_{1-2}\cdot \cos(0) = 0

N1−2⋅1=0N_{1-2}\cdot 1 = 0

Rzutowanie na oś Y

N1−2⋅sin⁡(0)+(−0.5)⋅sin⁡(90)+(−0.5)⋅sin⁡(−90)=0N_{1-2}\cdot \sin(0) + (-0.5)\cdot \sin(90) + (-0.5)\cdot \sin(-90) = 0

N1−2⋅0+(−0.5)⋅1+(−0.5)⋅(−1)=0N_{1-2}\cdot 0 + (-0.5)\cdot 1 + (-0.5)\cdot (-1) = 0

−0.5+0.5=0-0.5 + 0.5 = 0

Równanie X

N1−2⋅1=0N_{1-2}\cdot 1 = 0

Równanie Y

=0= 0

Wynik

Wyliczono N1−2=0kN\text{Wyliczono } N_{1-2} = 0 kN

Wybrano węzeł 2:

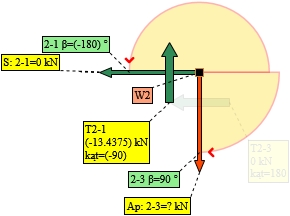
Rys. 13. Analiza węzła 2 - schemat

Do policzeniaN2−3,β=90\text{Do policzenia} N_{2-3}, \beta = 90

PoliczoneN2−1=0,β=−180\text{Policzone} N_{2-1}=0, \beta = -180

Rzutowanie na oś X

N2−3⋅cos⁡(90∘)=0N_{2-3} \cdot \cos(90^\circ) = 0

N2−3⋅0=0N_{2-3} \cdot 0 = 0

Rzutowanie na oś Y

N2−3⋅sin⁡(90)+(−0.5)⋅sin⁡(−90)=0N_{2-3} \cdot \sin(90) + (-0.5)\cdot \sin(-90) = 0

N2−3⋅1+(−0.5)⋅(−1)=0N_{2-3} \cdot 1 + (-0.5)\cdot (-1) = 0

N2−3⋅1+0.5=0N_{2-3} \cdot 1 + 0.5 = 0

Równanie X

=0= 0

Równanie Y

N2−3⋅1+0.5=0N_{2-3} \cdot 1 + 0.5 = 0

Wynik

Wyliczono N2−3=−0.5kN\text{Wyliczono } N_{2-3} = -0.5 kN

Wykres N:

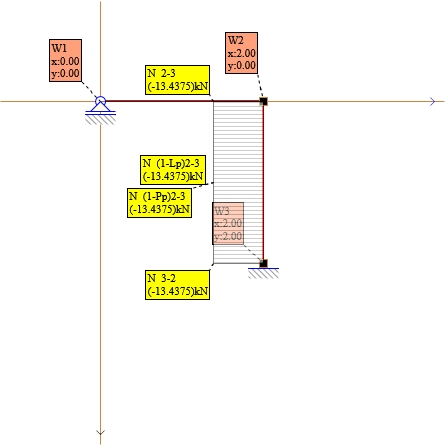
Rys. 14. Wykres N

13. Obliczenie reakcji podporowych

Aby węzeł był w równowadze, suma jego składowych sił i reakcji rzutowana na oś X i oś Y musi być równa zero:

∑Sx+∑Rx+∑Px=0\sum Sx + \sum Rx + \sum Px = 0∑Sy+∑Ry+∑Py=0\sum Sy + \sum Ry + \sum Py = 0

Gdzie:

  • ΣSx - suma sił prętowych rzutowana na oś X w węźle
  • ΣRx - suma reakcji podporowych rzutowana na oś X w węźle (jeżeli istnieje)
  • ΣPx - suma oddziaływania zewnętrznego rzutowana na oś X w węźle (jeżeli jest przyłożona)
  • ΣSy - suma sił prętowych rzutowana na oś Y w węźle
  • ΣRy - suma reakcji podporowych rzutowana na oś Y w węźle (jeżeli istnieje)
  • ΣPy - suma oddziaływania zewnętrznego rzutowana na oś Y w węźle (jeżeli jest przyłożona)

Wybrano węzeł 1:

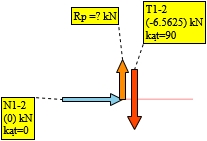
Rys. 15. Reakcje w węźle 1 - schemat

Do policzeniaRP1,β=(−90)\text{Do policzenia} R_{P_1}, \beta = (-90)

PoliczoneS2−1=0,β=0\text{Policzone} S_{2-1}=0, \beta = 0

Rzutowanie na oś X

RP1⋅cos⁡(−90)=0R_{P_1} \cdot \cos(-90) = 0

RP1⋅0=0R_{P_1} \cdot 0 = 0

Rzutowanie na oś Y

RP1⋅sin⁡(−90)+6.5625⋅sin⁡(90)=0R_{P_1} \cdot \sin(-90) + 6.5625 \cdot \sin(90) = 0

RP1⋅−1+6.5625⋅1=0R_{P_1} \cdot -1 + 6.5625 \cdot 1= 0

Równanie X

=0= 0

Równanie Y

RP1⋅−1+6.5625 kNR_{P_1} \cdot -1 + 6.5625 \text{ kN}

Wynik

Wyliczono RP1=6.5625 kN\text{Wyliczono } R_{P_1} = 6.5625 \text{ kN}

Wybrano węzeł 3:

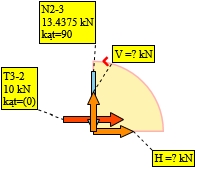
Rys. 17. Reakcje w węźle 3 - schemat

Do policzeniaH3,β=0\text{Do policzenia} H_{3}, \beta = 0

Do policzeniaV3,β=−90\text{Do policzenia} V_{3}, \beta = -90

PoliczoneS3−2=(−13.4375),β=−90\text{Policzone} S_{3-2}=(-13.4375), \beta = -90

Rzutowanie na oś X

H3⋅cos⁡(0)+V3⋅cos⁡(−90)+(−10)⋅cos⁡(0)=0H_{3} \cdot \cos(0) + V_{3} \cdot \cos(-90) + (-10) \cdot \cos(0) = 0

H3⋅1+V3⋅0+(−10)⋅1=0H_{3} \cdot 1 + V_{3} \cdot 0 + (-10) \cdot 1 = 0

H3⋅1+(−10)=0H_{3} \cdot 1 + (-10) = 0

Rzutowanie na oś Y

H3⋅sin⁡(0)+V3⋅sin⁡(−90)+13.4375⋅sin⁡(90)=0H_{3} \cdot \sin(0) + V_{3} \cdot \sin(-90) + 13.4375 \cdot \sin(90) = 0

H3⋅0+V3⋅(−1)+13.4375⋅1=0H_{3} \cdot 0 + V_{3} \cdot (-1) + 13.4375 \cdot 1 = 0

V3⋅(−1)+13.4375=0V_{3} \cdot (-1) + 13.4375= 0

Układ równań

{H3⋅1⋅(−10)=0V3⋅(−1)+13.4375=0\begin{cases} H_{3} \cdot 1 \cdot (-10) = 0 \\ V_{3} \cdot (-1) + 13.4375 = 0 \end{cases}

Wynik

Wyliczono H3=10 kN\text{Wyliczono } H_{3} = 10 \text{ kN}

Wyliczono V3=13.4375 kN\text{Wyliczono } V_{3} = 13.4375 \text{ kN}

Reakcje podporowe:

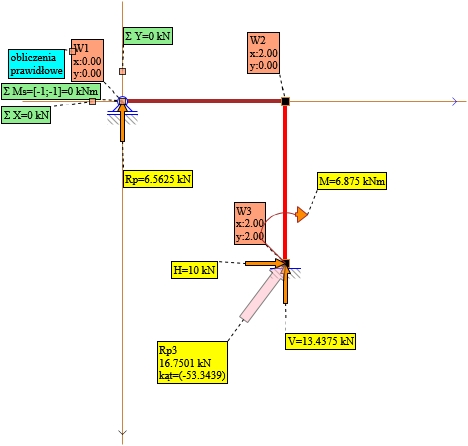
Rys. 16. Reakcje podporowe

14. Sprawdzenie reakcji podporowych - moment

Sprawdzenia poprawności wyznaczenia reakcji podporowych dokonamy w punkcie [(-1); (-1)] w układzie XY.

Punkt musi być tak dobrany, aby wszystkie siły i reakcje brały udział w obliczaniu sumy momentów.

W punkcie tym suma momentów od wszystkich sił i reakcji powinna wynosić M = 0:

∑M=RP1⋅(0−(−1))⋅sin⁡(−90)+V3⋅(2−(−1))+H3⋅−1−2+\sum M = R_{P_1} \cdot (0 - (-1)) \cdot \sin(-90) + V_3 \cdot (2 - (-1)) + H_3 \cdot -1 - 2 +

+M3+P0⋅(−1−1)⋅cos⁡(180)+Q0y⋅(1−(−1))⋅sin⁡(90)++ M_3 + P_0 \cdot (-1 - 1) \cdot \cos(180) + Q_{0y} \cdot (1 - (-1)) \cdot \sin(90) +

+M0=0+ M_{0} = 0∑M=6.5625⋅1⋅(−1)+(−13.4375)⋅3+10⋅(−3)+6.875+10⋅(−2)⋅(−1)+\sum M = 6.5625 \cdot 1 \cdot (-1) + (-13.4375) \cdot 3 + 10 \cdot (-3) + 6.875 + 10 \cdot (-2) \cdot (-1) +

+20⋅2⋅1+10=0+ 20 \cdot 2 \cdot 1 + 10 = 0∑M=6.5625⋅(−1)+(−13.4375)⋅3+10⋅(−3)+6.875+10⋅2+20⋅2+\sum M = 6.5625 \cdot (-1) + (-13.4375) \cdot 3 + 10 \cdot (-3) + 6.875 + 10 \cdot 2 + 20 \cdot 2 +

+10=0+ 10 = 0∑M=(−6.5625)+(−40.3125)+(−30)+6.875+20+40+10=0\sum M = (-6.5625) + (-40.3125) + (-30) + 6.875 + 20 + 40 + 10 = 0∑M=0 kNm\sum M = 0\ \text{kNm}

15. Sprawdzenie reakcji podporowych - rzut X

∑X=10+10⋅cos⁡(180)=0\sum X = 10 + 10 \cdot \cos(180) = 0∑X=10+10⋅(−1)=0\sum X = 10 + 10 \cdot (-1) = 0∑X=10+(−10)=0\sum X = 10 + (-10) = 0∑X=0 kN\sum X = 0\ \text{kN}

16. Sprawdzenie reakcji podporowych - rzut Y

∑Y=6.5625⋅sin⁡(−90)+(−13.4375)+20⋅sin⁡(90)=0\sum Y = 6.5625 \cdot \sin(-90) + (-13.4375) + 20 \cdot \sin(90) = 0∑Y=6.5625⋅(−1)+(−13.4375)+20⋅1=0\sum Y = 6.5625 \cdot (-1) + (-13.4375) + 20 \cdot 1 = 0∑Y=(−6.5625)+(−13.4375)+20=0\sum Y = (-6.5625) + (-13.4375) + 20 = 0∑Y=0 kN\sum Y = 0\ \text{kN}

17. Ocena wyników obliczeń

Z uwagi na spełnione warunki:

∑M=0.0,∑X=0.0,∑Y=0.0\sum M = 0.0, \quad \sum X = 0.0, \quad \sum Y = 0.0

Ocena: obliczenia prawidłowe

18. Sprawdzenie kinematyczne

Sprawdzamy, czy przemieszczenia w poszczególnych punktach spełniają warunki podparcia i ciągłości. Wystarczy sprawdzić tyle składowych, ile wynosi SSN (Stopień Statycznej Niewyznaczalności).

Przekształcamy schemat naszego układu na statycznie wyznaczalny poprzez redukcję nadliczbowych więzów. W miejscach usuniętych nadliczbowych przykładamy kolejno obciążenia jednostkowe i wyznaczamy momenty zginające.

Obciążenia jednostkowe dla kątów obrotu mają charakter momentów jednostkowych. Obciążenia jednostkowe dla przemieszczeń liniowych mają charakter sił jednostkowych. Przemieszczenia wynikowe obliczamy ze wzoru Maxwella-Mohra.

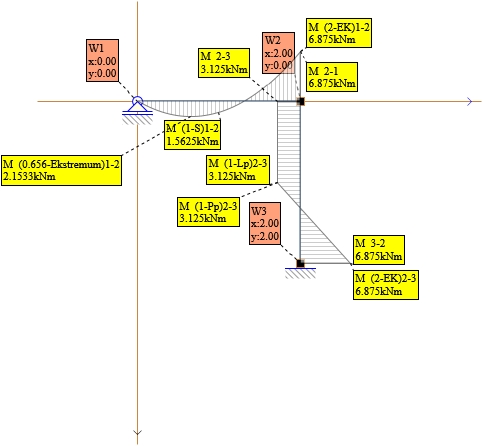
Rys. 17. Wykres M

19. Obliczenie układu podstawowego dla X₁

Działa tylko X₁.

Sprawdzono poprawność obliczeń dla schematu statycznego.

Pręt 1-2: Mik = 0, Mki = 1

Pręt 2-3: Mik = (-1), Mki = 1

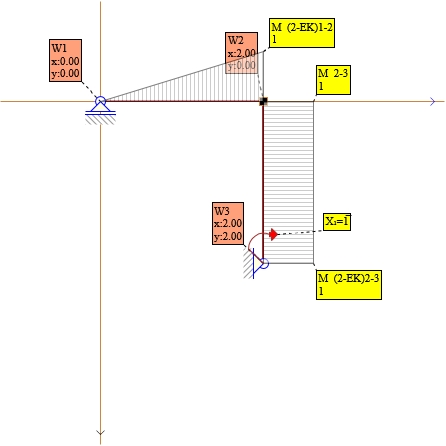
Rys. 18. Momenty dla X₁

20. Suma współczynników kontrolnych

Składnik M obciążenie:

[Δ1PΔ2P]\begin{bmatrix} \Delta_{1P} \\ \Delta_{2P} \end{bmatrix}

Δ1P=−0.6182+1.8682+(−3.125)+(−0.4882)+2.3632=−0.0000000011EI m\Delta_{1P} = -0.6182 + 1.8682 + (-3.125) + (-0.4882) + 2.3632 = -0.000000001\frac{1}{EI} \text{ m}

=0 m=0 \text{ m}

Suma współczynników pomiarowych: [0]

Obliczenia dokonane w programie Metor.

Ostatnia aktualizacja:
Oś Obojętna i Mimośrodowe RozciąganieMetoda Sił - podejście Maxwella-Mohra