Kącik Wiedzy
Kratownica - Metoda Równoważenia Węzłów krok po kroku

Kratownica - Metoda Równoważenia Węzłów krok po kroku

kwietnia 10, 2018

Zadanie: Dla kratownicy statycznie wyznaczalnej obliczyć reakcje podporowe i wyznaczyć metodą równoważenia węzłów siły w prętach.

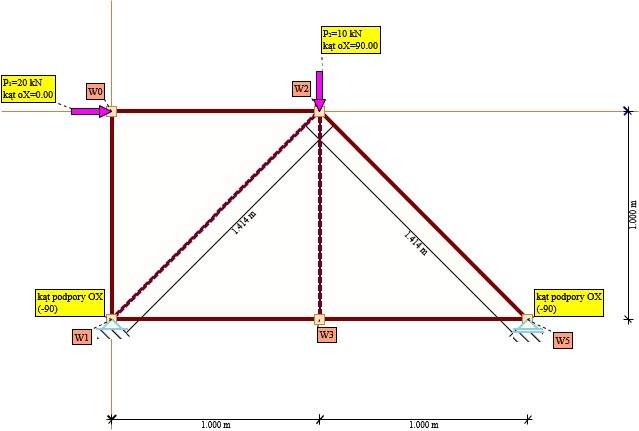
Rys. 1. Schemat kratownicy

1. Ustalenie warunku statycznej niewyznaczalności układu

Warunek konieczny geometrycznej niezmienności i statycznej wyznaczalności kratownicy o strukturze prostej:

p=2w−rp = 2w - r

gdzie:

  • pp = liczba prętów kratownicy
  • ww = liczba węzłów kratownicy
  • rr = liczba stopni swobody odbieranych przez podpory

Kratownica:

p=7,w=5p = 7, \quad w = 52w−r=2⋅5−3=72w - r = 2 \cdot 5 - 3 = 7

Warunek: 7=77 = 7, warunek jest spełniony.

2. Obliczenie kątów nachylenia prętów do osi X (wariant z sin i cos)

Pręt Nr 1-2 = (-45)°

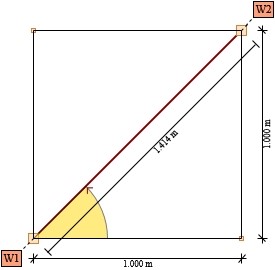
sin⁡α=YL=11.4142=0,7071\sin\alpha = \frac{Y}{L} = \frac{1}{1.4142} = 0{,}7071cos⁡α=XL=11.4142=0,7071\cos\alpha = \frac{X}{L} = \frac{1}{1.4142} = 0{,}7071

Rys. 2. Kąt nachylenia pręta 1-2

Pręt Nr 2-5 = 45°

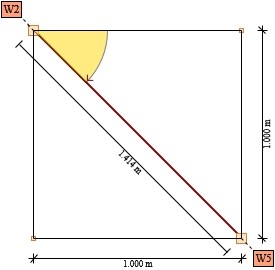
sin⁡α=YL=11,4142=0,7071\sin\alpha = \frac{Y}{L} = \frac{1}{1{,}4142} = 0{,}7071cos⁡α=XL=11,4142=0,7071\cos\alpha = \frac{X}{L} = \frac{1}{1{,}4142} = 0{,}7071

Rys. 3. Kąt nachylenia pręta 2-5

3. Wyznaczenie reakcji podporowych

Siły i reakcje będziemy przyjmować za dodatnie, gdy są skierowane zgodnie z układem osi XY, za ujemne, gdy są skierowane niezgodnie z układem osi XY. Będziemy rzutować siły i reakcje na oś X i oś Y wyliczając odpowiednie składowe rzutów:

Px=P⋅cos⁡(β)P_x = P \cdot \cos(\beta)Py=P⋅sin⁡(β)P_y = P \cdot \sin(\beta)

gdzie β\beta to kąt zawarty pomiędzy siłą lub reakcją a osią X, na podstawie tego kąta można określić zwrot siły lub reakcji.

Uwalniamy daną kratownicę od więzów i wyznaczamy reakcje podporowe.

Ogólne warunki równowagi:

∑M=0,∑X=0,∑Y=0\sum M = 0, \quad \sum X = 0, \quad \sum Y = 0
3.1. Suma momentów
∑M=0\sum M = 0

Suma wszystkich momentów od składowych reakcji i obciążeń siłowych w punkcie, w którym Moment = 0. Przyjmujemy punkt, w którym znajduje się podpora przegubowa, w tym punkcie Moment = 0.

∑M=RP5⋅(2−0)⋅sin⁡(−90)+P1(1−0)⋅cos⁡(0)+P2⋅(1−0)⋅sin⁡(90)=0\sum M = R_{P_5} \cdot (2-0) \cdot \sin(-90) + P_1(1-0) \cdot \cos(0) + P_2\cdot (1-0) \cdot \sin(90) = 0∑M=RP5⋅2⋅(−1)+20⋅1⋅1+10⋅1⋅1=0\sum M = R_{P_5} \cdot 2 \cdot (-1) + 20 \cdot 1 \cdot 1 + 10 \cdot 1 \cdot 1 = 0∑M=RP5⋅(−2)+20⋅1+10⋅1=0\sum M = R_{P_5} \cdot (-2) + 20 \cdot 1 + 10 \cdot 1 = 0∑M=RP5⋅(−2)+20+10=0\sum M = R_{P_5} \cdot (-2) + 20 + 10 = 0∑M=RP5⋅(−2)+30=0\sum M = R_{P_5} \cdot (-2) + 30 = 0RP5=15 kNR_{P_5} = 15\ \mathrm{kN}
3.2. Suma sił w kierunku X
∑X=0\sum X = 0

Suma wszystkich składowych reakcji i obciążeń siłowych rzutowana na oś X:

∑X=H1+P1⋅cos⁡(0)=0\sum X = H_1 + P_1 \cdot \cos(0) = 0∑X=H1+20⋅1=0\sum X = H_1 + 20 \cdot 1 = 0∑X=H1+20=0\sum X = H_1 + 20 = 0H1=(−20) kNH_1 = (-20)\ \mathrm{kN}
3.3. Suma sił w kierunku Y
∑Y=0\sum Y = 0

Suma wszystkich składowych reakcji i obciążeń siłowych rzutowana na oś Y:

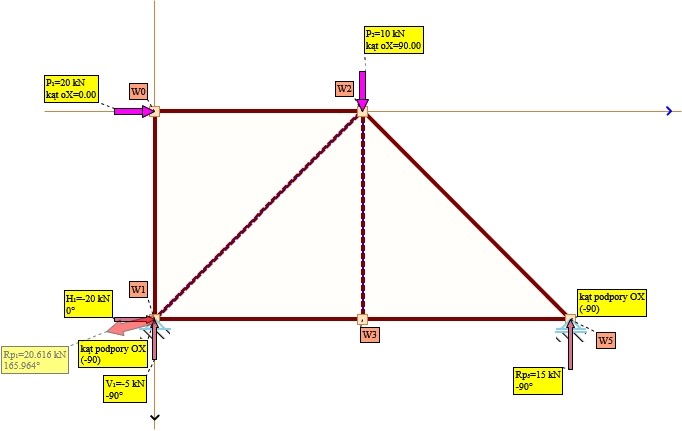
∑Y=−V1+P2⋅sin⁡(90)+RP5⋅sin⁡(−90)=0\sum Y = -V_1 + P_2 \cdot \sin(90) + R_{P_5} \cdot \sin(-90) = 0∑Y=−V1+10⋅1+15⋅(−1)=0\sum Y = -V_1 + 10 \cdot 1 + 15 \cdot (-1) = 0∑Y=−V1+10+(−15)=0\sum Y = -V_1 + 10 + (-15) = 0V1=(−5) kNV_1 = (-5)\ \mathrm{kN}

Rys. 4. Reakcje podporowe

4. Sprawdzenie reakcji podporowych

Sprawdzenia poprawności wyznaczenia reakcji podporowych dokonamy w punkcie [(-1);(-1)] w naszym układzie XY (punkt musi być tak dobrany, aby wszystkie siły i reakcje brały udział w obliczaniu Sumy Momentów). W punkcie tym Suma Momentów od wszystkich sił i reakcji powinna wynosić M=0M = 0.

∑M=0\sum M = 0

Suma wszystkich momentów od składowych reakcji i obciążeń siłowych w punkcie, w którym Moment = 0:

∑M=RP5⋅(2−(−1))⋅sin⁡(−90)+H1(−1−1)⋅cos⁡(0)+V1⋅(0−(−1))+\sum M = R_{P_5} \cdot (2-(-1)) \cdot \sin(-90) + H_1(-1-1) \cdot \cos(0) + V_1 \cdot (0-(-1)) ++P1⋅(−1−0)⋅cos⁡(0)+P2⋅(1−(−1))⋅sin⁡(90)=0+ P_1 \cdot (-1-0) \cdot \cos(0) + P_2 \cdot(1-(-1)) \cdot \sin(90) = 0∑M=15⋅3⋅(−1)+(−20)⋅(−2)+5⋅1+20⋅(−1)+10⋅2⋅1=0\sum M = 15 \cdot 3 \cdot (-1) + (-20) \cdot (-2) + 5 \cdot 1 + 20 \cdot (-1) + 10 \cdot 2 \cdot 1 = 0∑M=15⋅(−3)+(−20)⋅(−2)+5⋅1+20⋅(−1)+10⋅2=0\sum M = 15 \cdot (-3) + (-20) \cdot (-2) + 5 \cdot 1 + 20 \cdot (-1) + 10 \cdot 2 = 0∑M=0 kNm\sum M = 0\ \mathrm{kN}\mathrm{m}

5. Sprawdzenie reakcji podporowych - rzut X

∑X=H1+P1⋅cos⁡(0)=0\sum X = H_1 + P_1 \cdot \cos(0) = 0∑X=(−20)+20⋅1=0\sum X = (-20) + 20 \cdot 1 = 0∑X=(−20)+20=0\sum X = (-20) + 20 = 0∑X=0 kN\sum X = 0\ \mathrm{kN}

6. Sprawdzenie reakcji podporowych - rzut Y

∑Y=RP5⋅sin⁡(−90)+V1+P2⋅sin⁡(90)=0\sum Y = R_{P_5} \cdot \sin(-90) + V_1 + P_2 \cdot \sin(90) = 0∑Y=15⋅(−1)+5+10⋅1=0\sum Y = 15 \cdot (-1) + 5 + 10 \cdot 1 = 0∑Y=(−15)+5+10=0\sum Y = (-15) + 5 + 10 = 0∑Y=0 kN\sum Y = 0\ \mathrm{kN}

7. Obliczenie kątów nachylenia prętów do osi X (wariant z tan)

Xb−XaX_b - X_a i Yb−YaY_b - Y_a to różnica pomiędzy współrzędnymi końca pręta.

Pręt Nr 0-2 = 0°

arctan⁡(Yb−YaXb−Xa)=arctan⁡(0−01−0)=arctan⁡(01)=0°\arctan\left(\frac{Y_b - Y_a}{X_b - X_a}\right) = \arctan\left(\frac{0-0}{1-0}\right) = \arctan\left(\frac{0}{1}\right) = 0°

Pręt Nr 2-3 = 90°

arctan⁡(Yb−YaXb−Xa)=arctan⁡(1−01−1)=arctan⁡(10)=90°\arctan\left(\frac{Y_b - Y_a}{X_b - X_a}\right) = \arctan\left(\frac{1-0}{1-1}\right) = \arctan\left(\frac{1}{0}\right) = 90°

Pręt Nr 1-3 = 0°

arctan⁡(Yb−YaXb−Xa)=arctan⁡(1−11−0)=arctan⁡(01)=0°\arctan\left(\frac{Y_b - Y_a}{X_b - X_a}\right) = \arctan\left(\frac{1-1}{1-0}\right) = \arctan\left(\frac{0}{1}\right) = 0°

Pręt Nr 1-0 = (-90)°

arctan⁡(Yb−YaXb−Xa)=arctan⁡(0−10−0)=arctan⁡(−10)=(−90)°\arctan\left(\frac{Y_b - Y_a}{X_b - X_a}\right) = \arctan\left(\frac{0-1}{0-0}\right) = \arctan\left(\frac{-1}{0}\right) = (-90)°

Pręt Nr 3-5 = 0°

arctan⁡(Yb−YaXb−Xa)=arctan⁡(1−12−1)=arctan⁡(01)=0°\arctan\left(\frac{Y_b - Y_a}{X_b - X_a}\right) = \arctan\left(\frac{1-1}{2-1}\right) = \arctan\left(\frac{0}{1}\right) = 0°

Pręt Nr 2-5 = 45°

arctan⁡(Yb−YaXb−Xa)=arctan⁡(1−02−1)=arctan⁡(11)=45°\arctan\left(\frac{Y_b - Y_a}{X_b - X_a}\right) = \arctan\left(\frac{1-0}{2-1}\right) = \arctan\left(\frac{1}{1}\right) = 45°

Pręt Nr 1-2 = (-45)°

arctan⁡(Yb−YaXb−Xa)=arctan⁡(0−11−0)=arctan⁡(−11)=(−45)°\arctan\left(\frac{Y_b - Y_a}{X_b - X_a}\right) = \arctan\left(\frac{0-1}{1-0}\right) = \arctan\left(\frac{-1}{1}\right) = (-45)°

8. Obliczenie sił w prętach

Aby węzeł był w równowadze to suma jego składowych sił i reakcji rzutowana na oś X i oś Y musi być równa zero:

∑Nx+∑Rx+∑Px=0\sum N_x + \sum R_x + \sum P_x = 0∑Ny+∑Ry+∑Py=0\sum N_y + \sum R_y + \sum P_y = 0

gdzie:

∑Nx\sum N_x

- to suma sił prętowych rzutowana na oś X w węźle

∑Rx\sum R_x

- to suma reakcji podporowych rzutowana na oś X w węźle (jeżeli istnieje)

∑Px\sum P_x

- to suma odziaływania zewnętrznego rzutowana na oś X w węźle (jeżeli jest przyłożona)

∑Ny\sum N_y

- to suma sił prętowych rzutowana na oś Y w węźle

∑Ry\sum R_y

- to suma reakcji podporowych rzutowana na oś Y w węźle (jeżeli istnieje)

∑Py\sum P_y

- to suma odziaływania zewnętrznego rzutowana na oś Y w węźle (jeżeli jest przyłożona)

Obliczenia rozpoczynamy od węzła, dla którego liczba niewiadomych sił w prętach jest najmniejsza i wynosi maksymalnie 2.

Węzeł nr 0

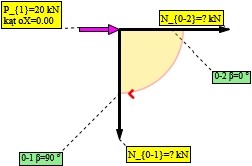
Rys. 5. Węzeł nr 0

Do policzenia: N0−2N_{0-2}, β=0°\beta = 0°

Do policzenia: N0−1N_{0-1}, β=90°\beta = 90°

Rzutowanie na oś X:

N0−2⋅cos⁡(0)+N0−1⋅cos⁡(90)+P1⋅cos⁡(0)=0N_{0-2} \cdot \cos(0) + N_{0-1} \cdot \cos(90) + P_1 \cdot \cos(0) = 0N0−2⋅1+N0−1⋅0+20⋅1=0N_{0-2} \cdot 1 + N_{0-1} \cdot 0 + 20 \cdot 1 = 0N0−2⋅1+20=0N_{0-2} \cdot 1 + 20 = 0

Rzutowanie na oś Y:

N0−2⋅sin⁡(0)+N0−1⋅sin⁡(90)=0N_{0-2} \cdot \sin(0) + N_{0-1} \cdot \sin(90) = 0N0−2⋅0+N0−1⋅1=0N_{0-2} \cdot 0 + N_{0-1} \cdot 1 = 0N0−2⋅0+N0−1⋅1=0N_{0-2} \cdot 0 + N_{0-1} \cdot 1 = 0

Układ równań:

{N0−2⋅1+20=0N0−2⋅+N0−1⋅1=0\begin{cases} N_{0-2} \cdot 1 + 20 = 0 \\ N_{0-2} \cdot + N_{0-1} \cdot 1 = 0 \end{cases}

Wynik:

N0−2=(−20) kNN_{0-2} = (-20)\ \mathrm{kN}N0−1=0 kNN_{0-1} = 0\ \mathrm{kN}
Węzeł nr 5

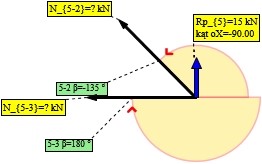
Rys. 6. Węzeł nr 5

Do policzenia: N5−2N_{5-2}, β=(−135)°\beta = (-135)°

Do policzenia: N5−3N_{5-3}, β=180°\beta = 180°

Rzutowanie na oś X:

N5−2⋅cos⁡(−135)+N5−3⋅cos⁡(180)=0N_{5-2} \cdot \cos(-135) + N_{5-3} \cdot \cos(180) = 0N5−2⋅(−0,7071)+N5−3⋅(−1)=0N_{5-2} \cdot (-0{,}7071) + N_{5-3} \cdot (-1) = 0N5−2⋅(−0,7071)+N5−3⋅(−1)=0N_{5-2} \cdot (-0{,}7071) + N_{5-3} \cdot (-1) = 0

Rzutowanie na oś Y:

N5−2⋅sin⁡(−135)+N5−3sin⁡(180)+RP5⋅sin⁡(−90)=0N_{5-2} \cdot \sin(-135) + N_{5-3} \sin(180) + R_{P_5} \cdot \sin(-90) = 0N5−2⋅(−0,7071)+N5−3⋅0+15⋅(−1)=0N_{5-2} \cdot (-0{,}7071) + N_{5-3} \cdot 0 + 15 \cdot (-1) = 0N5−2⋅(−0,7071)+(−15)=0N_{5-2} \cdot (-0{,}7071) + (-15) = 0

Układ równań:

{N5−2⋅(−0,7071)+N5−3⋅(−1)=0N5−2⋅(−0,7071)+(−15)=0\begin{cases} N_{5-2} \cdot (-0{,}7071) + N_{5-3} \cdot (-1) = 0 \\ N_{5-2} \cdot (-0{,}7071) + (-15) = 0 \end{cases}

Wynik:

N5−2=(−21,2132) kNN_{5-2} = (-21{,}2132)\ \mathrm{kN}N5−3=15 kNN_{5-3} = 15\ \mathrm{kN}
Węzeł nr 1

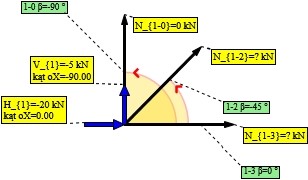
Rys. 7. Węzeł nr 1

Do policzenia: N1−2N_{1-2}, β=(−45)°\beta = (-45)°

Do policzenia: N1−3N_{1-3}, β=0°\beta = 0°

Policzone: N1−0=0 kNN_{1-0} = 0\ \mathrm{kN}, β=(−90)°\beta = (-90)°

Rzutowanie na oś X:

N1−2⋅cos⁡(−45)+N1−3⋅cos⁡(0)+H1=0N_{1-2} \cdot \cos(-45) + N_{1-3} \cdot \cos(0) + H_1 = 0N1−2⋅0,7071+N1−3⋅1+(−20)=0N_{1-2} \cdot 0{,}7071 + N_{1-3} \cdot 1 + (-20) = 0N1−2⋅0,7071+N1−3⋅1+(−20)=0N_{1-2} \cdot 0{,}7071 + N_{1-3} \cdot 1 + (-20) = 0

Rzutowanie na oś Y:

N1−2⋅sin⁡(−45)+N1−3⋅sin⁡(0)+V1=0N_{1-2} \cdot \sin(-45) + N_{1-3} \cdot \sin(0) + V_1 = 0N1−2⋅(−0,7071)+N1−3⋅0+5=0N_{1-2} \cdot (-0{,}7071) + N_{1-3} \cdot 0 + 5 = 0N1−2⋅(−0,7071)+5=0N_{1-2} \cdot (-0{,}7071) + 5 = 0

Układ równań:

{N1−2⋅0,7071+N1−3⋅1+(−20)=0N1−2⋅(−0,7071)+5=0\begin{cases} N_{1-2} \cdot 0{,}7071 + N_{1-3} \cdot 1 + (-20) = 0 \\ N_{1-2} \cdot (-0{,}7071) + 5 = 0 \end{cases}

Wynik:

N1−2=7,0711 kNN_{1-2} = 7{,}0711\ \mathrm{kN}N1−3=15 kNN_{1-3} = 15\ \mathrm{kN}
Węzeł nr 2

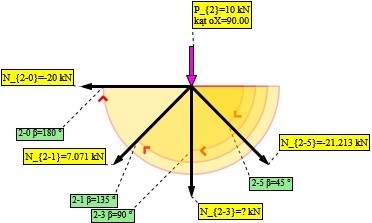
Rys. 8. Węzeł nr 2

Do policzenia: N2−3N_{2-3}, β=90°\beta = 90°

Policzone: N2−0=(−20) kNN_{2-0} = (-20)\ \mathrm{kN}, β=180°\beta = 180°

Policzone: N2−5=(−21,2132) kNN_{2-5} = (-21{,}2132)\ \mathrm{kN}, β=45°\beta = 45°

Policzone: N2−1=7,0711 kNN_{2-1} = 7{,}0711\ \mathrm{kN}, β=135°\beta = 135°

Rzutowanie na oś X:

N2−3⋅cos⁡(90)+N2−0⋅cos⁡(180)+N2−5⋅cos⁡(45)+N2−1⋅cos⁡(135)=0N_{2-3} \cdot \cos(90) + N_{2-0} \cdot \cos(180) + N_{2-5} \cdot \cos(45) + N_{2-1} \cdot \cos(135) = 0N2−3⋅0+(−20)⋅(−1)+(−21,2132)⋅0,7071+7,0711⋅(−0,7071)=0N_{2-3} \cdot 0 + (-20) \cdot (-1) + (-21{,}2132) \cdot 0{,}7071 + 7{,}0711 \cdot (-0{,}7071) = 0N2−3⋅0+20+(−15)+(−5)=0N_{2-3} \cdot 0 + 20 + (-15) + (-5) = 0

Rzutowanie na oś Y:

N2−3⋅sin⁡(90)+P2⋅sin⁡(90)+N2−5⋅sin⁡(45)+N2−1⋅sin⁡(135)=0N_{2-3} \cdot \sin(90) + P_2 \cdot \sin(90) + N_{2-5} \cdot \sin(45) + N_{2-1} \cdot \sin(135) = 0N2−3⋅1+10⋅1+(−21,2132)⋅0,7071+7,0711⋅0,7071=0N_{2-3} \cdot 1 + 10 \cdot 1 + (-21{,}2132) \cdot 0{,}7071 + 7{,}0711 \cdot 0{,}7071 = 0N2−3⋅1+10+(−15)+5=0N_{2-3} \cdot 1 + 10 + (-15) + 5 = 0

Równanie:

N2−3⋅0+0=0N_{2-3} \cdot 0 + 0 = 0

lub równanie:

N2−3⋅1+0=0N_{2-3} \cdot 1 + 0 = 0

Wynik:

N2−3=0 kNN_{2-3} = 0\ \mathrm{kN}

9. Zestawienie wszystkich sił w prętach

PrętN [kN]kąt [°]L [m]funkcja
0-2-20.00000.00001.0000ściskany
2-30.000090.00001.0000jest zerowy
1-315.00000.00001.0000rozciągany
0-10.000090.00001.0000jest zerowy
3-515.00000.00001.0000rozciągany
2-5-21.213245.00001.4142ściskany
1-27.0711-45.00001.4142rozciągany

Zadanie zostało wygenerowane w programie Kratos.

Ostatnia aktualizacja:
Obliczanie sił w węzłach kratownic metodą RitteraKratownica - Metoda Rittera krok po kroku