Elipsa Bezwładności
Wprowadzenie
Elipsa bezwładności jest graficzną reprezentacją rozkładu bezwładności geometrycznej przekroju w różnych kierunkach. Długości promieni elipsy w poszczególnych kierunkach odpowiadają promieniom bezwładności przekroju względem osi o tych kierunkach. Elipsa bezwładności jest konstruowana na podstawie głównych centralnych momentów bezwładności przekroju.
Definicja promienia bezwładności
Promień bezwładności jest to pierwiastek kwadratowy z ilorazu osiowego momentu bezwładności i pola powierzchni przekroju:
Gdzie:
- , – promienie bezwładności (półosie elipsy bezwładności)
- , – główne centralne momenty bezwładności
- – pole powierzchni przekroju
Przykład obliczeniowy
Teraz wykonamy obliczenia dla przykładu nr 2 (cały przykład możesz zobaczyć w artykule Momenty bezwładności - przykład nr 2).
Dane do obliczeń
Z przykładu nr 2 mamy następujące dane:
Obliczenie promieni bezwładności
Maksymalny promień bezwładności:
Minimalny promień bezwładności:
Graficzna reprezentacja elipsy bezwładności
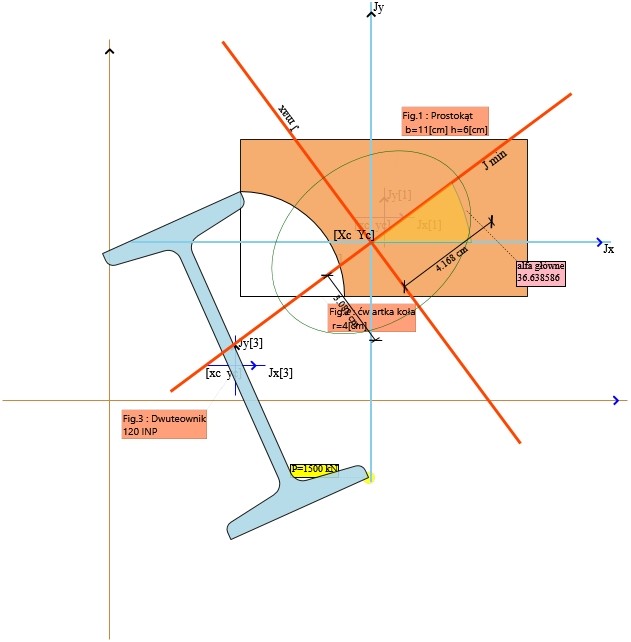
Rys. 1. Elipsa bezwładności dla układu figur z przykładu nr 2
Na rysunku przedstawiono elipsę bezwładności nałożoną na układ figur. Półosie elipsy odpowiadają obliczonym promieniom bezwładności:
- Większa półoś elipsy:
- Mniejsza półoś elipsy:
Podsumowanie
Elipsa bezwładności stanowi graficzną interpretację zmienności promienia bezwładności przekroju w zależności od kierunku osi. Jej główne własności są następujące:
- Półosie elipsy odpowiadają promieniom bezwładności i ,
- Kierunki półosi pokrywają się z głównymi centralnymi osiami bezwładności przekroju,
- Większa półoś odpowiada kierunkowi większego momentu bezwładności, a tym samym większej sztywności przekroju na zginanie,
- Elipsa bezwładności obrazuje zmianę promienia bezwładności przy obrocie układu współrzędnych,
- Znajomość elipsy bezwładności jest istotna przy projektowaniu elementów konstrukcyjnych pracujących na zginanie w różnych płaszczyznach.